Magische Quadrate: Geschichte

---

Magische Quadrate sind keine Erfindung neuzeitlicher Algebraiker und Zahlentheoretiker. Zahlenschemata, die besondere Eigenschaften aufweisen, sind schon lange bekannt. Die überraschenden arithmetischen Eigenschaften der magischen Quadrate ließen frühere Kulturen auf besondere magische Kräfte schließen. Hier begegneten sich Kult und Numerologie. Die Anziehungskraft numerologischer Praktiken scheint ungebrochen, wie zahlreiche aktuelle Veröffentlichungen belegen. Es kann davon ausgegangen werden, daß auch heute noch magische Quadrate ihren Stellenwert in der Astrologie haben. Erlaubt ist, was gefällt, und geeignet ist, dem zahlungswilligen Kunden das Geld aus der Tasche zu locken.

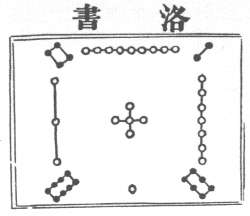
Bei Endres/Schimmel lesen wir: "Es gibt eine Anekdote über die Entdeckung des ersten magischen Quadrates: Im alten China regierte von 2205 bis 2198 v.Chr. ein gerechter und weiser Herrscher, der Kaiser Yü, der sein Reich mit großer Umsicht verwaltete. Konfuzius berichtet, der Kaiser sei einmal damit beschäftigt gewesen, Dämme zu bauen, um den Überschwemmungen des gelben Flusses Einhalt zu tun. Als er in Gedanken versunken war, erschien ihm die göttliche Schildkröte, die den Namen Hi trug. Auf dem Rücken der Schildkröte war eine Figur gezeichnet, die mit Zahlzeichen versehen war." (Das Mysterium der Zahl S.44). Eine alte, wenngleich nicht so alte Abbildung sei hier wiedergegeben.

In heutiger Schreibweise sieht dieses magische Quadrat, das "Lo Shu" mit der Kantenlänge 3 so aus:

Abgesehen von Drehungen und Spiegelungen ist das Lo Shu das einzige echte magische Quadrat der Kantenlänge 3. Den Besonderheiten dieses Quadrates ist hier eine eigene Seite gewidmet. Laut Martin Gardner gehört die vorhin wiedergegebene Anekdote ins Reich der Legende, denn nach heutiger Gelehrtenmeinung datiert das Lo Shu nicht vor dem 4.Jhdt.v.Chr. Vgl. dazu Time Travel and other Mathematical Bewilderments, S.215. Gericke zitiert in der Geschichte der Mathematik als Gewährsmann Joseph Needham, der die Datierung nicht vor das 5. Jhdt. v.Chr. legt.

Den arithmetischen Magischen Quadraten nahestehend sind quadratische Aufschreibungen magischer Sprüche, wie z.B. die seit der Antike bekannte Sator-Formel. Diese Formel kann zeilen- und spaltenweise gelesen werden. Darüberhinaus ist sie auch rückwärts zeilen- wie spaltenweise lesbar und stellt damit ein Palindrom dar. Die Papyrussammlung der österreichischen Nationalbibliothek in Wien zeigt in ihrer Ausstellung ein Exemplar, das über 2000 Jahre alt ist.

Diese Anordnung diente als Talisman gegen Krankheiten, besonders gegen die Tollwut. Dazu schreibt Frischbier 1870 in seinem Werk Hexenspruch und Zauberbann: "Im Samlande schreibt man die gegen den Biß eines tollen Hundes mitgetheilte Form SATOR auf ein Stück Zinn, setzt oben, unten, rechts und links Kreuze, umreitet damit dreimal das Feuer, wirft das Zinn im Namen des dreieinigen Gottes in die Flamme und jagt schnell davon" (S.110).
Außerdem sollte die Sator-Formel zum Eindämmen von Bränden nützlich sein. Bis in das 18. Jhdt. sind amtliche Verordnungen, z.B. aus Sachsen bekannt, die vorschrieben, Holzteller mit dieser Formel vorrätig zu halten, um sie in brennende Gebäude zu werfen.

Magische Quadrate mit mehrfach gleichartig belegten Zellen sind älter als solche mit Zelleninhalten, die komplett unterschiedlich belegt sind. Hier sei insbesondere auf den Aufsatz von Schuster Magische Quadrate im islamischen Bereich verwiesen. Auf S.20 stellt der Autor ein Zauberquadrat dieser Struktur vor - und nimmt damit unbewußt Bezug auf die Lateinischen Quadrate:

a	b	c
c	a	b
b	c	a

In Indien und Korea wurden magische Quadrate an den Außenwänden von Tempeln angebracht. Die frühesten bekannten datieren aus dem 12. Jhdt.

Berühmt ist Albrecht Dürers Kupferstich Melencholia, der ein magisches Quadrat der Kantenlänge 4 zeigt. Bemerkenswert ist die unterste Zeile des Quadrates: die beiden mittleren Felder enthalten die Zahlen 15 und 14, die zusammen gelesen das Entstehungsjahr des Holzschnittes angeben. Diese Abbildung zeigt das erste bekannte magische Quadrat im Abendland.

Ausschnitt aus Dürers Melencholia
Hervorhebung des magischen Quadrates
Warum ist die "5" kopfstehend?

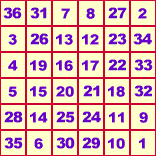
Michael Stifel (1487[?] - 19.4.1567), Freund Luthers, war Pastor zu Wittenberg, später Annaberg, nicht nur Theologe, sondern auch Rechenmeister ersten Ranges. Michael Stifel setzte sich in seiner Arithmetica integra intensiv mit dem Wesen der natürlichen, gebrochenen und irrationalen Zahlen auseinander und legte mit seinen Vorarbeiten das Fundament zu den Arbeiten Briggs' und Napiers über die Logarithmen. Die Ausführungen Stifels zu den Rahmenquadraten werden an geeigneter Stelle diskutiert. Stifel bringt in seinem Rechen Bichlein vom End Christ ein magisches Quadrat der Kantenlänge 6 (vgl. Gericke II S 243). Er stellt fest, daß die Summe aller Zahlen des Quadrates 666 ist - die berühmt-berüchtigte Zahl des Tiers.

Den Quadraten unterschiedlicher Kantenlängen wurden spezifische Eigenschaften zugeschrieben; nicht zuletzt deshalb wurden Amulette angefertigt, die zur Verstärkung ihrer Wirkung magische Quadrate enthielten. Um 1540 verfertigte Cornelius Agrippa von Nettesheim magische Quadrate der Kantenlängen 3 bis 9 und ordnete ihnen die damals bekannten "Planeten" zu. In der Literatur geistern seither Abbildungen von magischen Talismanen herum; ihren Ursprung zurückzuverfolgen, ist nahezu unmöglich. Die hier gezeigten Abbildungen entstammen W. Ahrens, Mathematische Spiele, S.82-83. Eine größere Sammlung solcher Amulette findet sich bei Paul Heimbach.

Saturnamulett, Kantenlänge 3. Von Drehung abgesehen, identisch mit dem Lo Shu

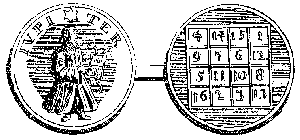Jupiteramulett, Kantenlänge 4

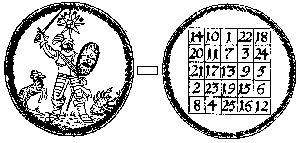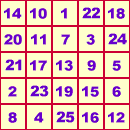
Marsamulett, Kantenlänge 5

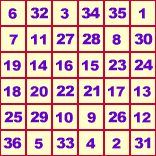
Sonnenamulett, Kantenlänge 6

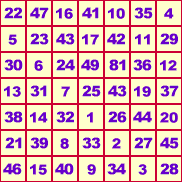
Venusamulett, Kantenlänge 7

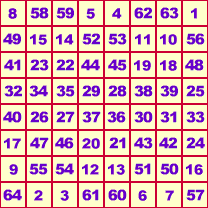
Merkuramulett, Kantenlänge 8

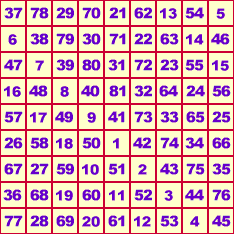Mondamulett, Kantenlänge 9

Agrippa von Nettesheim schafft auch einem Bezug zwischen Zahlensymbolik und dem Körper des Menschen. Die Ähnlichkeit des Diagrammes mit der klassischen quadratischen Darstellung eines Horoskopes ist sicher nicht zufällig.

Um 1590 erscheinen in einem chinesischen Druckwerk magische Quadrate der Kantenlängen 6 und 7. Man kann davon ausgehen, daß hier ein seit langen bekanntes Wissen veröffentlicht wurde.

Die jesuitischen Unversalgelehrten Athanasius Kircher (2.5.1601-30.10.1680) und Gaspar Schott (5.2.1608-22.5.1666) untersuchten ebenfalls magische Quadrate. Kircher war einer der ersten im Abendland, die sich systematisch mit magischen Quadraten befaßten. In seiner Arithmologica zeigt er unter anderem auch das Lo Shu.

In seiner Technica Curiosa zeigt Schott, basierend auf Aufzeichnungen Kirchers, mehrere magische Quadrate, darunter auch das Lo Shu. Bemerkenswert ist, daß Schott die Konstruktion magischer Quadrate gerader Kantenlänge beschreibt.

Der französische Forschungsreisende de LaLoubère (1642-1729) beschrieb in seine Buch Du Royaume de Siam 1693 eine Konstruktionsmethode für ungerade magische Quadrate, die er dort erlernte. Wir werden das Verfahren im mathematischen Teil verallgemeinern.

Überhaupt war das siebzehnte Jahrhundert eine Zeit des Fortschrittes der Wissenschaften und nicht zuletzt auch der Mathematik. Die magischen Quadrate fanden gebührende Aufmerksamkeit und erste systematische Theorien wurden veröffentlicht. Hier sind insbesondere die Herren Frénicle de Bessy, de LaHire und Claude Bachet de Mézeriac zu nennen, deren Arbeiten heute noch lesenswert sind.

Auch in Goethes Faust findet sich eine Anspielung auf magische Quadrate:

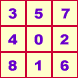
T. Pakraduny weiß in seinem Werk Die Welt der geheimen Mächte (vgl. S.750) die nachstehenden Quadrate wiederzugeben. Leider macht der Autor keine näheren Angaben zu den Besonderheiten und Hintergründen um das Achter-Quadrat.

"Natürliches" Quadrat		Magisches Quadrat Identisch Lo Shu		Hexen-Quadrat In der Hauptdiagonalen keine magische Konstante 15		Achter-Quadrat Nicht magisch, Rahmensummen = 15

Das Hexen-Quadrat lehnt sich an das "Hexeneinmaleins an. Doch dieses steht dem "Baum des Sefirot" erheblich näher, als dem magischen Quadrat.

Baum des Sefirot nach Anthanasius Kircher
Oedipus Aegyptiacus II,1 S. 289

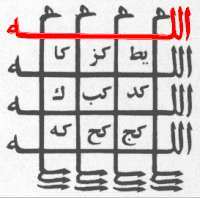
Auch in jüngerer Zeit wurden Magische Quadrate - ihrer vermeintlichen magischen Wirkung wegen verwendet. In den Kulturen des nahen Ostens sind zahlenmythische Verfahren verbreiteter als bei uns. Ein schönes Beispiel dafür ist dieses Quadrat:

Arabisches Magisches Quadrat mit der magischen Summe 66. Hervorhebung: Allah = 66. Vgl. Ifrah, Universalgeschichte der Zahlen, S. 350. Bei Ifrah ist das Schema um 90° verdreht wiedergegeben!

Man beachte die rechten und unteren Begrenzungen des Quadrates, die den Namen Allah darstellen, dessen Ziffernsumme (Schriftzeichen werden als Zahlzeichen verwendet) die magische Summe 66 ergibt.

Benjamin Franklin (17.1.1706-17.4.1790) befaßte sich in seiner Jugend eingehend mit magischen Quadraten. Im gesetzten Alter kehrte er wieder zu dieser Freizeitbeschäftigung zurück. Franklin veröffentlichte einige Quadrate mit besonderen Eigenschaften. In die Reihe derer, die das Thema beschäftigte, kann Leonhard Euler (15.4.1707-18.9.1783) gestellt werden. Euler verdanken wir auch eine Grundlage der Theorie der griechisch-lateinischen Quadrate, die in einem Exkurs näher beschrieben sind.

Mit Hilfe des Computers konnten magische Quadrate mit viefältigen, besonderen Eigenschaften entdeckt werden.

weiter im Text