Ungerade Magische Quadrate

---

Magische Quadrate, deren Kantenlänge eine ungerade Zahl ist, lassen sich konstruktiv am einfachsten anfertigen. Am Beispiel des 5 ´ 5 -Quadrates werden hier die bekanntesten Konstruktionsverfahren erläutert.

Die Methode von Bachet

Diese Methode, sie wird auch "indische Methode" genannt, wird eingehend von Bischoff beschrieben. Manche Autoren geben dem Verfahren aus naheliegenden Gründen den Namen "Treppenhausmethode" oder "Terrassenmethode".
Man geht von einem leeren 5 ´ 5 -Feld aus und setzt an jeder Seite eine dreieckige Anordnung von Feldern an. Danach werden systematisch die Zahlenwerte von 1 bis n², in unserem Beispiel 25, von oben beginnend, in diagonaler Abfolge in die freien Felder geschrieben. Auf diese Weise bleibt jedes zweite Feld ungenutzt.

Im nächsten Schritt werden die an den Seiten angesetzten Teile auf die jeweils gegenüberliegende Lücke verschoben. Fertig!

Die ungeraden natürlichen magischen Quadrate, die nach dieser Methode konstruiert werden, haben zusätzliche Eigenschaften:

• Summe zweier harmonischer Felder = n² + 1
• Am Schema eines ungeraden magischen Quadrates lassen sich die restlichen Werte für die vier Eckfelder, das Mittelfeld und die vier, dem Mittelfeld benachbarten Felder angeben:

n2 - n + 2 2 n + 1 2 n2   n   n2 + 1 2 n2 - n + 1 1 2n2 - n + 1 2 n2 + n 2

 Die Methode von de LaLoubère

De LaLoubère war ein französischer Gesandter, der 1687-1688 im Auftrage Ludwigs XIV in Siam¹ weilte. In seinem Buch Du royaume de Siam beschrieb er das hier wiedergegebene Verfahren. De LaLoubère führte den Begriff des "carrée magique" in die französche Sprache ein.

Die Methode geht von einem leeren Quadratschema aus und benutzt folgendes Regelwerk:

1. Das Quadratschema wird als allseitig zyklisch geschlossen betrachtet.
2. Startfeld ist das Mittelfeld der obersten Zeile.
3. Die Felder werden diagonal fortlaufend nach rechts oben numeriert.
   • Wenn der Rand des Quadrates erreicht wird, wird zyklisch geschlossen fortgesetzt.
   • Wenn ein bereits belegtes Feld oder das rechte obere Eckfeld erreicht werden, wird um 1 Feld senkrecht nach unten fortgesetzt.

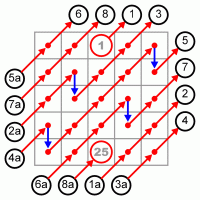Eine Verallgemeinerung dieses und des vorangegangenen Verfahrens findet sich im formalen Teil.

 Die Methode von de LaHire

De La Hires Verfahren bedient sich zweier Hilfsquadrate, die anfangs leer sind. Die Diagonale des ersten Quadrates wird von links oben nach rechts unten beliebig mit den Ziffern 1 bis 5 belegt; lediglich die 3 bzw. "mittlere" Zahl von 1 bis n muß im Mittelfeld stehen. Anschließend werden die Gegendiagonalen mit denselben Zahlenwerten aufgefüllt, die durch die eingetragenen Werte gegeben sind. Hierbei bleiben einige Diagonalfelder frei. Deswegen werden beim Auffüllen die Diagonalen als zyklisch geschlossen aufgefaßt, d.h. beim Erreichen eines Randes des Quadratschemas wird die Fortsetzung der gebrochenen Diagonalen ebenfalls mit der entsprechenden Zahl gefüllt.

1. Schritt Belegen der Hauptdiagonalen		2.Schritt: Auffüllen der Gegendiagonalen		3. Schritt Ergänzen der gebrochenen Gegendiagonalen

In ähnlicher Weise wird das zweite Hilfsquadrat ausgefüllt. Hier beginnt das Verfahren mit der Gegendiagonalen. Die einzufüllenden Werte sind 0, n, 2n usw., wobei der "mittlere" Wert wieder im Mittelfeld plaziert werden muß. Danach werden in gleicher Weise wie beim ersten Hilfsquadrat die Diagonalen bzw. gebrochenen Diagonalen befüllt.

1. Schritt Belegen der Gegendiagonalen		2.Schritt: Auffüllen der Hauptdiagonalen		3. Schritt Ergänzen der gebrochenen Hauptdiagonalen

Die Zelle [i,j] des resultierenden Quadrates entsteht durch die Addition der jeweiligen Zellen [i,j] der Hilfsquadrate.

Durch zellenweise Addition entsteht das magische Quadrat

Eine anschauliche Darstellung, warum dieses Verfahren alle Zahlen von 1 bis n² liefert, gibt Ahrens in seinem Werk Mathematische Unterhaltungen und Spiele, S. 216. Zugleich kann die Methode auch zur Konstruktion magischer Quadrate verwendet werden. Zu diesem Zweck werden zwei Kreisscheiben konzentrisch drehbar angeordnet. Die eine Scheibe trägt die Zahlen 1..n, die andere die Werte 0, n, 2n...n²-n.

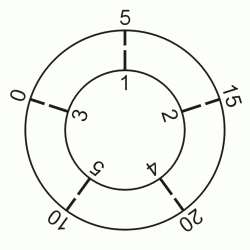
Abgelesen wird immer konsequent an gleicher Position beginnend. Z.B. wird an der senkrechten Position begonnen und im Uhrzeigersinn abgelesen. Die Summen der jeweils gegenüberliegenden Werte werden in die erste Zeile des Quadratschemas eingetragen. In diesem Falle sind das 6, 17, 24, 15, 3. Anschließend wird die innere Scheibe um 1/5 nach rechts, die äußere Scheibe um 1/5 nach links verdreht. Danach kann die zweite Zeile des Quadrates befüllt werden, wobei erneut an der senkrechten Position abgelesen wird. Ablesen und Summenbildung werden n mal wiederholt, bis das Quadrat vollständig befüllt ist.

 Der Horizont

Der Horizont, der die Sicht beschränkt, ist manchmal durch eine ungünstige Darstellungsweise gegeben. Wir können uns überlegen, was passiert, wenn wir die Zellen eines magischen Quadrates nicht im Dezimalsystem befüllen, sondern im Zahlensystem zu Basis n, wenn n die Kantenlänge des Quadrates darstellt. Die Struktur wird besonders offenbar, wenn die Einträge bei 0 beginnen, statt wie üblich bei 1:

5 ´ 5-Quadrat, konstruiert nach LaLoubère, dezimal

5 ´ 5-Quadrat, konstruiert nach LaLoubère, dargestellt zur Basis 5

Die Änderung der Sichtweise enthüllt, daß Magische Quadrate auch kombinatorisch betrachtet werden können. Bereits das Verfahren von de LaHire arbeitet mit einer kombinatorischen Sytematik. Mehr davon im Exkurs. zu den eulerschen Quadraten.

weiter im Text