Die magische Eigenschaft der Magischen Quadrate ist erstaunlich genug. Umso mehr überrascht, daß die Konstruktion von Magischen Quadraten möglich ist, die zusätzliche Eigenschaften haben. Wir betrachten hier die sog. pandiagonalen und die symmetrischen Quadrate etwas eingehender.
| Definition | Ein pandiagonales magisches Quadrat der Kantenlänge n ist ein magisches Quadrat, dessen Summen der Zellen in den gebrochenen Diagonalen ebenfalls die magische Zahl m ergeben. Pandiagonale Quadrate werden auch als Teufelsquadrate bezeichnet. |
|---|
Da man sich unter gebrochenen Diagonalen nur schwer etwas vorstellen kann, ist es einfacher, neben das magische Quadrat ein zweites, identisches zu schreiben. Wenn jetzt alle Diagonalen die magische Zahl ergeben, ist das Quadrat pandiagonal.
Fertigt man aus einem solchen Quadrat eine "Tapete" an, so ist jedes beliebige 5´5-Quadrat, das aus dieser Tapete ausgewählt wird, magisch.
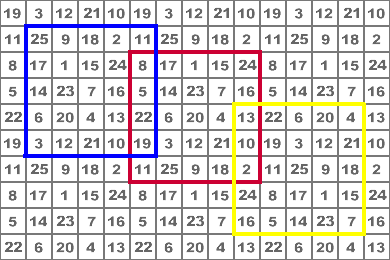
| Definition | Ein symmetrisches magisches Quadrat der Kantenlänge n ist ein magisches Quadrat, bei dem je zwei zur Mittenfeld bzw. Mittelpunkt punktsymmetrisch liegende Zellen (auch harmonische Felder genannt) die Summe n2+1 haben |
|---|
Ungerade magische Quadrate, die nach den Methoden von Bachet und de La Loubère erzeugt wurden, sind symmetrisch. Symmetrisch ist auch das "Dürer"-Quadrat:
| Das Quadrat aus Düürers Holzschnitt Melancholia |
Vgl. dazu auch die allgemeinen Formeln für magische Quadrate der Kantenlänge 4.
| weiter im Text |
| Stand: 11.12.2006 / |
|