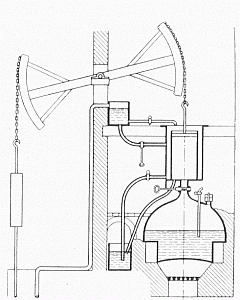
Schnitt durch eine Newcomen-Maschine (1712)
Matschoss, Die Entwicklung der Dampfmaschine I, S.305, Fig.47
Thermodynamik kommt so manchem Laien wie schwarze Magie vor. Sicher, dieser
Zweig der Physik bedient sich häufig raffinierter mathematischer Verfahren,
und Computermodelle für Verbrennungsvorgänge in Motoren sind alles
andere als einfach. Da Thermodynamik auch auf statistische Methoden
zurückgreift, denken manche Perpetuum-Mobile-Erfinder, hier ließe
sich ein Schlupfloch finden, um die Physik zu überlisten. Es sollte
uns bewußt sein, daß der zweite Hauptsatz der Thermodynamik eine
statistische Aussage darstellt.
Versuchen wir eine Basis-Thermodynamik im Schnelldurchgang, denn das hier
soll kein Lehrbuch der Physik werden, sondern ein Einblick in die Analyse
thermodynamischer Perpetua Mobilia!
Viele physikalische Zusammenhänge werden durch eine idealisierte Beschreibung erst erkennbar und lassen sich ausreichend einfach darlegen. Die Theorie der Gase war bis zu Robert Priestleys Zeit relativ unentwickelt und alles andere als einheitlich. Es war ein schwieriger Weg zur Erkenntnis, daß unterschiedliche Arten "Luft" existieren und daß die Theorie des Phlogistons zugunsten eines auf Sauerstoff basierenden Modells der Verbrennungsvorgänge aufgegeben werden mußte. Systematische Untersuchungen zeigten, daß Gase trotz unterschiedlicher chemischer Eigenschaften physikalische Eigenschaften haben, die innerhalb gewisser Grenzen gleichartig sind. Man abstrahiert von den konkreten Gasen und gelangt zu der Modellvorstellung des idealen Gases. In der Praxis kommt z.B. Helium diesem Ideal ziemlich nahe.
Auf Robert Boyle (25.01.1627-30.12.1691) und Edme Mariotte (ca.1620-12.05.1684) geht die Beschreibung eines physikalischen Zusammenhangs zurück, der heute als Boyle-Mariottesches Gesetz bezeichnet wird. Es beschreibt die Abhängigkeit von Druck und Volumen einer bestimmten Gasmenge bei konstanter Temperatur. In seiner modernen Fom lautet es:
p1 V1 = p2 V2
Ein zweiter Zusammenhang wird als Gesetz von Gay-Lussac bezeichnet. Es setzt konstanten Druck voraus und beschreibt, wie Temperatur und Volumen einer bestimmten Gasmenge voneinander abhängen:
V1 / V2 = T1 / T2
Darauf basierend und mit etwas Zusatzwissen läßt sich die sogenannte universelle Gasgleichung formulieren:
Wer bis hierher aufmerksam gelesen hat, sollte sich fragen, was die Faktoren n und R bedeuten. n ist die Anzahl der Gasteilchen und R ist eine Proportionalitätskonstante, die als Rydbergkonstante oder universelle Gaskonstante bezeichnet wird. Sie wurde experimentell zu yyy bestimmt. Hier begegnet uns zum ersten Mal eine statistische Aussage, denn die Formel besagt dreierlei:
Erste praktische Anwendungen, die auf dem Boyle-Mariotteschen Gesetz basierten, waren Kolben-Vakuumpumpen und frühe Dampfmaschinen. Speziell die Maschine von Thomas Newcomen (getauft 28.02.1663-5.8.1729) ist geeignet, den Sachverhalt zu erklären.

Schnitt durch eine Newcomen-Maschine (1712)
Matschoss, Die Entwicklung der
Dampfmaschine I, S.305, Fig.47
Die Newcomen-Maschinen waren, ebenso wie die verbesserten Nachfolgekonstruktionen Smeatons, atmosphärische Maschinen. Sie nutzen allein den Luftdruck, nicht jedoch die Kraft des Dampfes, zur Gewinnung mechanischer Arbeit. Das Prinzip der Maschine ist einfach:
Maschinen wie diese arbeiteten mit sehr schlechtem Wirkungsgrad (1%-3%) und waren dennoch gut genug, um in den englischen Kohlegruben halbwegs wirtschaftlich eingesetzt zu werden.1 Die wesentlichen Mängel der Newcomen-Maschine sind:
Es bedurfte der beharrlichen Forschungsarbeit James Watts (19.01.1736-19.08.1819), um die unvollkommene Newcomen-Maschine in eine effektive Arbeitsmaschine weiterzuentwickeln. Möglich wurde das aber auch durch die Fortschritte des Maschinenbaus, der erst ausreichende Reife erreichen mußte. Oft wird behauptet, Watt habe seine Erfindung eher durch Zufall entdeckt. Das Gegenteil ist der Fall. Er erarbeitete systematische Versuche, um das Verhalten des gespannten Dampfes zu erforschen und zog daraus seine Schlüsse.
Die beiden Herren markieren Anfangs- und Endpunkt der Erkenntnis, daß es ein mechanisches Wärmeäquivalent gibt, d.h. Wärme und mechanische Arbeit sind mit festen Umrechnungsfaktoren (einheitenbezogen) ineinander transformierbar. Im Idealfall ist das verlustfrei möglich.
Benjamin Thompson (26.03.1753-21.08.1814) war eine etwas schillernde Persönlichkeit. In Amerika geboren, führten ihn ein weite Reisetätigkeit und Dienste bei verschiedenen Personen nach Bayern, wo er bei Graf Montgelas Kriegsminister war und das Münchner Zeughaus beaufsichtigte. Dort machte er die Beobachtung, daß Kanonenrohre beim Bohren so heiß werden, daß sich auf ihnen sogar ein Kessel Wasser kochen ließ. Das reichte zur Erkenntnis, daß man der Sache nachgehen müsse. Thompson löste sich von der Phlogistontheorie und formulierte eindeutig, daß Wärme ein nichtstoffliches, sondern ein energetisches Phänimen sei. Er bestimmte näherungsweise ein mechanisches Wärmeäquivalent. Julius Robert Mayer und James Prescott Joule konnten vierzig Jahre später mit einer präzisen Proportionalitätsbeziehung aufwarten, die im engeren Sinne heute als mechanisches Wärmeäquivalent bezeichnet wird.
Bei der Betrachtung thermodynamischer Prozesse spielen Zustandsübergänge eine entscheidende Rolle. Solche Übergänge können idealisiert betrachtet werden, was die Theorie erheblich vereinfacht. Klassisch sind diese vier Übergänge.
| Definition | Bei der isothermen Zustandsänderung wird die Temperatur T
konstant gehalten. Bei der isobaren Zustandsänderung wird der Druck des idealen Gases konstant gehalten. Die isochore Zustandsänderung erfolgt bei konstantem Volumen. Bei der adiabatischen Zustandsänderung wird angenommen, daß sich alle drei Zustandsgößen ändern können, daß aber kein Wärmeaustausch mit der Umgebung stattfinden soll. |
|
|---|---|---|
|
|
|
|
| Bemerkung | Diese Übergänge sind idealisierte Vorstellungen. In der Praxis wäre z.B. ein isothermer Übergang nicht durchführbar, da die Kompression von Gasen stets mit einer Temperaturerhöhung einhergeht, es sei denn, es stünde unendlich viel Zeit zur Verfügung. | |
Diese Begriffe sind für die Thermodynamik grundlegend, und wir werden sie in den nächsten Abschnitten noch benötigen. Die Eigenarten der Zustandsübergänge veranschaulicht man am einfachsten anhand von Diagrammen. Später werden sich diese Diagramme bei der Theorie der Kreisprozesse noch als sehr nützlich erweisen.
 |
 |
|
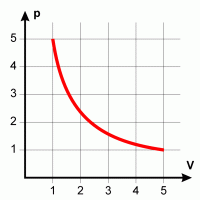
| Isothermer Übergang Bei konstanter Temperatur resultiert eine Hyperbel, da das Produkt p V konstant bleibt. |
Isobarer Übergang Eine Zustandsänderung, die den Druck konstant läßt, erfordert die gleichzeitige Änderung von Volumen und Temperatur. |
|
 |
 |
|
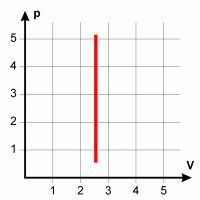
| Isochorer Übergang Konstantes Volumen erfordert die gleichzeitige Änderung von Druck und Temperatur, da V/T konstant bleiben muß. |
Adiabatischer Übergang Da kein Wärmeaustausch mit der Umgebung vorausgetzt ist, verläuft die Adiabate steiler als die Isotherme. |
Die Geschichte der modernen Thermodynamik ist eng mit dem Namen Carnot verbunden. Lazare Carnot (13.05.1753-02.08.1823) arbeitete neben seiner politischen Tätigkeit anf mathematischem und mechanischem Gebiet.
 |
Sadi (01.06.1796-24.08.1832), der Sohn Lazare Carnots, überflügelte den Ruhm seines Vaters beträchtlich, als er seine Schrift Réflexions sur la puissance motrice du feu et sur les machines propres à dévelloper cette puissance. veröffentlichte. Mit dieser Arbeit war die Basis der modernen Thermodynamik gelegt. Sadi Carnot hatte ganz bewußt die praktische Anwendbarkeit im Sinn, als er den Versuch unternahm, die Dampfmaschine theoretisch zu analysieren. Schon vor Julius Robert Mayer berechnete er ein mechanisches Wärmeäquivalent. Vor allem aber ermittelte er den maximal erreichbaren Wirkungsgrad einer Wärmekraftmaschine und wurde damit zu einem der Pioniere der Hauptsätze der Thermodynamik. |
Wärmekraftmaschinen arbeiten für gewöhnlich auf der Basis eines Kreisprozesses. Klassisch sind der Carnot- und der Stirling-Prozeß für Kolbenmaschinen. Der Einfachheit wegen beschränkt man sich für gewöhnlich anfangs auf eine Einzylindermaschine. Die Idee des Kreisprozesses ist einfach. Beginnend von einem Ausgangspunkt finden mehrere Zustandsübergänge des Gases statt, bis der Ausgangspunkt wieder erreicht ist.
|
|
|||||||||||||||||||||
Der Carnot-Prozeß
|
Der Stirling-Prozeß
|
Vergegenwärtigen wir uns die Bedeutung der Zustandsübergänge!
Es stellt sich heraus, daß eine Kraftmaschine, deren Arbeitsvolumen
sich nach einem dieser Kreisprozesse verändert, Arbeit zu leisten vermag.
Dies kommt dadurch zustande, daß thermische Energie in mechanische
Arbeit umgewandelt wird. Entscheidend für die Energieausbeute im Sinne
der nutzbaren Abgabeleistung, ist die Fläche, die von den begrenzenden
Zustandsübergängen umschlossen wird. Der Umlaufsinn ist ebenfalls
wichtig, denn von ihm hängt ab, ob die Fläche positiv oder negativ
bewertet wird. Anders ausgedrückt, ob die Maschine Arbeit leistet, oder
Arbeit "hineingesteckt" werden muß.
Die Umkehrung des Prozesses ist auf diese Weise auch möglich. In dem
Fall wird mechanische Arbeit in Wärme umgewandelt. Ein Effekt, den man
beobachten kann, wenn man einen Fahrradreifen mit der Handluftpumpe kräftig
aufpumpt: das Ventil erwärmt sich.
In der technischen Praxis wurden an Dampfmaschinen sog. Indikatoren angebaut, um ein Kreisdiagramm des tatsächlichen Prozesses zu gewinnen. Dieses Indikatordiagramm gab Auskunft darüber, wie effizient die untersuchte Maschine arbeitete. Das Indikatordiagramm ist, wie uns bereits vertraut, ein V-p-Diagramm.
 |
***image*** (H=300 pix) |
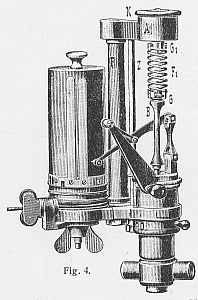
| Ein sogenannter Indikator Aus: Lueger, Lexikon der gesamten Technik, Bd. V, S. 178 |
Anordnung zur Gewinnung eines Indikatordiagramms. Ein kleiner Druckkolben bewegt den Schreibstift, der den momentanen Druck in der Höhe markiert. Der drehbare Zylinder, der das Papier trägt, ist mittels einer Schur mit der Kolbenstange verbunden. Da beim zylindrichen Kolben das Volumen direkt propertional zum Weg ist, resultiert auf dem Papier ein V-p-Diagramm. |
Wie dieses Diagramm auszusehen habe, wurde vorab aus den geforderten Rahmenbedingungen für die spezielle Maschine berechnet. Dazu bediente man sich graphischer Verfahren, Dampfexpansionstabellen und der universellen Gasgleichung. In der Praxis wurde geprüft, inwieweit sich die ausgeführte Maschine den berechneten Parameterwerten annäherte. Abweichungen des aufgezeichneten Diagrammes waren stets ein Hinweis auf Maschinen- oder Bedienfehler. Freilich konnte auch die Meßvorrichtung falsch angebracht oder eingestellt worden sein. Das Interpretieren von Indikatordiagrammen war fester Bestandteil der zünftigen Ingenieursausbildung.
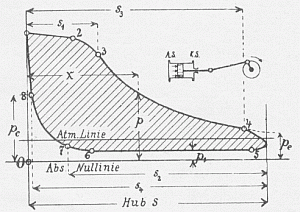 |
Idealisiertes Indikatordiagramm aus Barth,
Die Dampfmaschinen, II S. 19 Fig.7.
Barth unterscheidet acht ausgezeichnete Punkte beim Durchlaufen des
Kreisprozesses:
|
||||||||||||||||
 |
Berechnetes Indikatordiagramm einer praktisch auszuführenden Maschine, 1924. Die Erstellung des Diagramms orientiert sich an den Daten des Dampfdruckes, des Kolbenweges und des Schieberverhaltens (beachte dazu die halbkreisförmige, unterlegte Hilfsfigur!)2 | ||||||||||||||||
 |
Meßtechnisch gewonnenes Indikatordiagramm. Man beachte die Abweichungen der praktisch gewonnenen Kurve von den Idealdiagrammen! Die Ein- und Ausströmorgane werden zu ungeeigneten Zeitpunkten betätigt, woraus die Differenz zwischen der Ideallinie und der gemessenen Kurve resultiert. Aufschlußreich ist die Schleife auf der linken Seite des Diagramms. Diese Schleife hat als Flächenelement negativen Umlaufsinn, d.h. hier handelt es sich im Sinne der mechanischen Leistungsausbeute um Verluste.3 |
Es bleibt die Frage nach dem Nutzen der bisherigen Ausführungen und der Kreisdiagramme. Die Antwort ist schnell gegeben: Die Fläche des Diagramms kann maximal durch ein Rechteck beschrieben werden. Da in der Praxis ein Druck von p=0 nicht erreichbar ist, ist der Wirkungsgrad der thermischen Kraftmaschine stets kleiner als 100%. Dies bedeutet, daß ein Perpetuum Mobile auf dieser Basis nicht gebaut werden kann.
Die bisherigen Betrachtungen erfolgten alle unter der Voraussetzung, daß die Gase und Zustandsübergänge ideal sind. Die Praxis ist wie üblich nicht ideal. Reale Gase verhalten sich deutlich anders, als die hier beschriebenen idealisierten Modelle. Entwertet das nicht alles bisher Erarbeitete? Mitnichten. Bei ausreichend hohen Temperaturen dürfen reale Gase in der Praxis als ideal aufgefaßt werden; zumindest bei einfachen Anwendungen und Analysen.
Die bisherigen Erkennnisse sollten wir um gewisse Fakten erweitern, insbesondere diese:
Zur Veranschaulichung des Sachverhaltes noch ein paar Diagramme:
 |
Isothermen von Kohlendioxyd. Unterhalb einer gewissen Temperatur sind
die Isothermen keine Hyperbeln mehr, sondern Linien mit waagerechten und
senkrechten Komponenten. Dies erklärt sich aus der gleichzeitigen Existenz
von gasförmiger und flüssiger Phase ab einem gewissen Druck. Der
waagerechte Bereich der Isotherme geht in eine nahezu senkrechte Linie
über, wenn das gesamte Gasvolumen verflüssigt ist. Die rote Linie
kennzeichnet das Sättigungsgebiet, in dem flüssige und
gasförmige Phase gleichzeitig existieren können. Merke: Flüssigkeiten sind kaum kompressibel, weswegen sie unter Alltagsbedingungen als inkompressibel betrachtet werden dürfen. |
 |
Ein Temperatur-Druck-Diagramm von Wasserdampf. Unter geeigneten Bedingungen können sogar alle drei Aggregatszustände (gasförmig, fest, flüssig) gleichzeitig exisiteren. Die p,V,T-Konstellation, bei der dieser Effekt eintritt, wird als Tripelpunkt des Gases bezeichnet. Die Temperatur, oberhalb der unter keinen Umständen Kondensation erfolgt, nennt man kritische Temperatur. Der Punkt im T-p-Diagramm, bei dem die Dampfdichte und die die Dichte der flüssigen Phase gleich sind, heiß kritischer Punkt. |
 |
Helium hat keinen Tripelpunkt, sondern zeigt ein anderes Verhalten, da es zwei verschiedene flüssige Phasen hat. |
Bei der Verflüssigung von Gasen tritt das Phänomen auf, daß Gase sowohl in der flüssigen als auch in der gasförmigen Phase zugleich im Behälter vorhanden sind. Dies wird praktisch genutzt, wie das Beispiel des Gasfeuerzeuges oder der Campinggasflasche zeigt. Solange noch Gas in der flüssigen Phase vorhanden ist, ist der gasförmige Teil unter nahezu konstantem Druck. Andere Gase, wie z.B. Sauerstoff sind im technischen Sinne nicht so "gutmütig". Um eine nennenswerte Menge Sauerstoff in einem Behälter einzusperren, sind hohe Drücke erforderlich, bei denen sich der Sauerstoff nicht verflüssigt. Dazu muß zusätzlich die Temperatur entsprechend erniedrigt werden. Die vorangegangenen Beispieldiagramme zeigen, daß reale Gase sehr unterschiedliches Verhalten zeigen können.
Bis hierher war die Mathematik zur Thermodynamik nicht gerade schwierig. Das ändert sich schlagartig, wenn statistische Methoden eingeführt werden, um die oben gezeigten Phänomene zu beschreiben.
Maxwell Boltzmann Nernst Planck Szilard
Letztendlich kam durch die statistische Methode ans Licht, daß der zweite Hauptsatz der Thermodynamik als gesicherte Aussage betrachtet werden darf, zumindest im makroskopischen Bereich.
Wer mehr über dieses Thema lesen will, der sollte auf solide Literatur aus dem gymnasialen Oberstufenbereich und der universitäten Physik zurückgreifen. Dem angehenden Erfinder thermodynamischer Perpetua Mobilia sind die Werke von Kuhn, Föppl, Planck und Schüle gute Wegweiser.
1882 machte ein englischer Professor namens Sam Gamgee von sich reden, als er eine thermodynamische Maschine vorschlug, die sich die Verdampfung und Kondensation von Ammoniak zunutze machen sollte. Da Ammoniak einen Siedepunkt von -33,5°C4 bei atmosphärischem Druck hat, sollte diese Maschine bei Zimmertemperatur arbeiten, was gegenüber herkömmlichen Wärmekraftmaschinen einen erheblichen Vorteil darstellt. Zudem hat die Maschine einen geschlossenen Kreislauf; es gibt keine Abgase oder Neuzufuhr von Betriebsmitteln.
***image***
Gamgees Ammoniak-Motor
Auf den ersten Blick eine Art Dampfmaschine, die beim näheren Hinsehen ihre Besonderheit offenbart. In der Einströmphase bewegt sich der Kolben durch den Gasdruck und Expansion abwärts. Nach Schließen des Einströmventils epandiert das Ammoniak weiter, bis es kondensiert (merke: Expansion kühlt ein Gas ab!) und durch ein Auslaßventil mittels einer Pumpe wieder in den Kessel zurückgefördert wird. Ein Schwungrad sorgt für gleichmäßigen Gang, den Antrieb der Pumpe und die Steuerung der Ventile. Man beachte, daß im Kessel sowohl flüssige als auch gasförmige Phase des Ammonaik nebeneinander existieren und daß die Idee der Maschine darauf beruht, eine geringe Flüssigkeitsmenge gegen einen konstanten Gasdruck in den Behälter zu fördern.
Die ganze Angelegenheit klingt zu schön um wahr zu sein - die Maschine funktioniert nicht. Wer vorhin bei der Theorie ein wenig aufgepaßt hat, wird sehen, daß es sich hier um eine ganz gewöhnliche Kraftmaschine handelt, die folglich einen Wirkungsgrad von weniger als 100% haben muß.
Die Verkäufer von Maschinen und Rezepten, Wasser als Sprit für den Autoantrieb zu nutzen, finden immer noch genügend Dumme - zumindest scheint das Geschäft lukrativ zu sein, wie die Präsenz einiger Internetseiten beweist.
Interessanter sind da schon die Behauptungen mancher Erfinder, sie hätten eine Methode gefunden, Wasser ohne nennenswerten Energieaufwand in seine beiden Bestandteile zu zerlegen. Der solcherart gewonnene Wasserstoff bzw. Sauerstoff kann in einem Ottomotor verbrannt werden. Das ist die gängige Vorstellung, wie eine Freie-Energie-Maschine funktionieren könnte. Der Gedanke ist bestechend: Das Wasser kann im geschlossenen Kreislauf bleiben, so daß die Umwelt nicht belastet wird. Der Motor treibt nicht nur ein Auto an, sondern auch die Nebenaggregate, wie z.B. die Lichtmaschine, die den Strom für die Zerlegung des Wassers liefert. Was ist davon zu halten?
***image***
Ein Wasserzerlege-Perpetuum-Mobile.
Wasser läßt sich durch Elektrolyse in seine Bestandteile zerlegen, wie im schulischen Chemieunterricht demonstriert wird. Nach dem spektakulären Verbrennen der Gase unter kräftiger Geräuschentwicklung kommt meist die Theorie. Ab dieser Stelle haben dann die Wasserzerleger und die Käufer des Produkts nicht mehr richtig aufgepaßt. Sonst wüßten sie, daß die so gewonnene Energie nicht größer sein kann, als die zuvor aufgewendete elektrische Arbeit zum Zerlegen des Wasssers. Konventionell funktioniert die Sache nicht; sie wäre ein veritables Perpetuum Mobile.
Versuchen wir eine Analyse eines Elektrolyse-PMs!
***image***
yyy
Das hinderte Erfinder nicht daran, Patente für solche Thermo-Turbos zu beantragen. Ein Beispiel ist das yyy.
***image***
Eine perpetuierliche thermische Kraftmaschine
Doch es gibt die Verfechter der Freien Energie, die behaupten, sie könnten Wasser mit einem geringeren Energieeinsatz zerlegen, als mit der klassischen Methode. Den Beweis, daß sie dieses Kunststück in einem thermodynamisch geschlossenem System vollbringen können, blieben sie bis heute schuldig.
1. Schließlich hatte der Grubenbesitzer
nur die Wahl, seine Grube im Grundwasser versinken zu sehen oder sich am
Kohleverbrauch der Dampfmaschine zu ruinieren.
2. Studentenausarbeitung, Fach Maschinenbau
an der Technischen Hochschule München, 1924. Archiv des Autors.
3. Übungsaufgaben zum Indikator. Fach
Maschinenbau an der Technischen Hochschule München, 1924. Archiv des
Autors.
4. Daten nach D'Ans/Lax
Taschenbuch für Chemiker und
Physiker
| Stand: 23.02.2004 / |
|