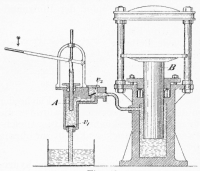
| "Heureka!" Archimedes, ca. 220 v.Chr. |
Langsam bin ich es leid, Auftriebsmaschinen zu analysieren, die angeblich Perpetua Mobilia darstellen. Zu zahlreich sind die Beispiele, zu einfach meist die Erklärung, warum sie nicht funktionieren können. Eines der aktuellsten Beispiele schickte mir ein Erfinder, der im Februar 2003 ein Patent für seine Maschine erhielt.
Der Gedanke, Auftriebskräfte für den Betrieb eines PM zu nutzen, ist alt, und Entwürfe gibt es zuhauf. Mein Archiv enthält mehrere hundert Maschinenentwürfe für Auftriebs-Perpetua Mobilia. Es gibt zwei Hauptklassen von Konstruktionsprinzipien:
So viele unterschiedliche Vorschläge und Erfindungen zum Thema Auftriebs-PM existieren mögen, sie basieren alle auf einer Handvoll von fehlgeleiteten Konzepten, die ich hier vorstelle.
Das mit dem Auftrieb ist eine seltsame Sache. Offenbar sind nur wenige
fähig, zu erklären, wie dieser Effekt zustandekommt. Auftrieb ist
etwas Geheimnisvolles und für Perpetua Mobilia attraktiv, da er wohl
irgendein verborgenes Prinzip nutzt. Doch es gibt kein Geheimnis, außer
der Tatsache, daß die meisten Erfinder von Auftriebs-Perpetua Mobilia
entweder in der Physikstunde nicht aufgepaßt haben, oder schlechte
Lehrer hatten. Keine der Alternativen ist ein guter Anfang, um Maschinen
zu konstruieren.
Hier finden Sie im Schnelldurchgang alles, was Sie über den Auftrieb
wissen sollten.
 |
Beginnen wir mit dem Druck. Druck wird definiert als Kraft pro Fläche. Üblicherweise findet man in Lehrbüchern den Hinweis, daß sich Druck gleichmäßig in Flüssigkeiten ausbreitet und daß die Druckkraft, die auf die Behälterwandungen wirkt (auch auf Gegenstände in der Flüssigkeit) überall gleich ist. Man illustriert das gern am Beispiel der hydraulischen Presse. Was Lehrbücher an dieser Stelle nicht immer schreiben: Der aufgewandte Druck wirkt gleichmäßig, doch es gibt noch eine zweite Einflußgröße, nämlich die Erdschwerkraft. Sie führt dazu, daß der Druck am Boden des Gefäßes höher ist als an der Oberfläche. |
Wie entsteht Auftrieb? Wenn ein Objekt teilweise oder ganz in eine Flüssigkeit eintaucht, dann wirkt Druck auf das Objekt. Druck wirkt in alle Richtungen und stets senkrecht auf die Oberflächen eines Objektes. Horizontale Kräfte, die in gleicher Höhe auf das Objekt wirken, kompensieren sich. Nur der senkrechte Anteil bewirkt eine resultierende Kraft, die der Erdschwerkraft entgegenwirkt und ein Objekt schwimmen läßt.
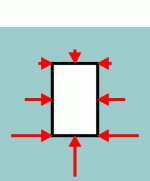 |
Wie wirkt der Flüssigkeitsdruck auf ein eingetauchtes Objekt? Genauso, wie ein Stapel Holzplatten immer schwerer wird, je höher er ist, ist die Last, die eine Flüssigkeitssäule darstellt, direkt von ihrer Höhe abhängig. Wir erinnern uns: Druck ist als Kraft pro Flächeneinheit definiert. Bei gleichbleibender Fläche nimmt der Druck linear mit der Flüssigkeitstiefe zu. In jeder waagerechten Schnittebene ist der Druck gleich, da die Flüssigkeit beweglich ist und ungleichmäßigen Kraftwirkungen solange ausweicht, bis Kräftegleichgewicht eintritt. |
Betrachten Sie die beiden nächsten Skizzen, um zu verstehen, wieso die Form bei gleichbleibendem Volumen keinen Einfluß auf die Auftriebskraft hat. Ein quaderförmiges Objekt sei untergetaucht. Wir nehmen an, daß die Dicke b (senkrecht zur Betrachtungsebene) des Objektes konstant ist. Das Objekt habe die Abmessungen a x 2a.
| Die Pfeile illustrieren die wirkenden Kräfte. Der Auftrieb errechnet sich aus der Höhendifferenz a und der Fläche, die auf einer Breite von 2a dem Druck ausgesetzt ist. Die wirksame Auftribskraft ist folglich 2a2 mal eine von der Dicke b des Objektes abhängige Konstante. | Die Dicke des Objektes hat sich nicht geändert. Die wirksame Auftriebskraft berechnet sich aus der doppelten Höhe des Objektes und der einfachen Breite, sodaß wieder eine Kraft wirkt, die von 2a2b bestimmt wird. Es bleibt folglich alles beim alten. |
Das ist für einfache quaderförmige Objekte unmittelbar einsichtig; doch die Behauptung gilt für Objekte beliebiger Form.
| *** to be expanded *** | Je nach Zielgruppe erklärt die physkalische Literatur die konstante Auftriebskraft bei konstantem Volumen des eingetauchten Objektes mit weniger oder mehr Mathematik. Bei unregelmäßig geformten Objekten sind diese Erklärungen nicht sehr anschaulich und benötigen erschreckend viele Integrale. Doch es gibt einen einfachen Trick, sich das Phänomen zu erklären. Man stelle sich einen Wassertank vor, der ein beliebig deformierbares Objekt enthält. Diese Objekt soll dieselbe Dichte wie Wasser haben. Ein mit Wasser (aber ohne Luft) zur teilweise gefüllter Luftballon kommt diesem Ideal sehr nahe. Das enthaltene Volumen V ist wegen der Inkompressibilität des Inhaltes und der umgebenden Flüssigkeit konstant. Der untergetauchte Ballon unterliegt unabhängig von seiner Form stets derselben Auftriebskraft, die seiner Gewichtskraft die Waage hält. Folglich schwebt dieses Objekt im Wasser. Da wir wissen, daß die Auftriebskraft nur von Volumen des eingetauchten Körpers abhängt, gilt der gleiche Zusammenhang auch für andere Objekte, selbst wenn sie nicht deformierbar sind wie der Luftballon im Besipiel. |
An dieser Stelle sollten Sie sich fragen, warum ich die Masse des eingetauchten Objektes bislang nicht berücksichtigt habe. Tatsächlich hängt die Auftriebskraft nicht von Form oder Masse ab, sondern nur vom Volumen des Objektes und der Dichte der Flüssigkeit.
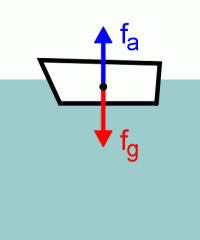
Wir alle sind mit der Tatsache vertraut, daß Boote für gewöhnlich schwimmen, Steine untergehen und U-Boote frei in Wasser beweglich sind. Diese unterschiedlichen Wirkungen hängen von der Dichte der Objekte ab, nicht aber von ihrer absoluten Masse. Betrachten wir die drei möglichen Fälle:
 |
 |
 |
| Dichte ist kleiner als die der Flüssigkeit Objekt schwimmt auf, da die Auftriebskraft des vollständig eingetauchten Objektes größer ist als seine Gewichtskraft. |
Dichte ist größer als die der
Flüssigkeit Objekt sinkt, da die Gewichtskraft größer ist als die Auftriebskraft. |
Dichte ist gleich der der Flüssigkeit Objekt schwebt, da sich Auftriebskraft und Gewichtskraft ausgleichen. |
Ein aufschwimmendes Objekt tut dies solange, bis es schwimmt. Ein Objekt schwimmt dann, wenn die auf das Objekt wirkende Auftriebskraft und die Gewichtskraft entgegengesetzt gleich sind. Das ist genau dann der Fall, wenn das verdrängte Flüssigkeitsvolumen der Masse des Objektes entspricht. Genauer: da im Schwerefeld die Gravitationskraft in gleicher Weise auf Flüssigkeit und Objekt wirken, sind auch die Kraftwirkungen gleichermaßen vorhanden. Ein schwimmendes Objekt taucht deswegen z.B. auf der Erde oder dem Mond gleich tief ein.
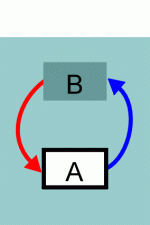 |
Ein spezifisch leichteres Objekt wird in einer Flüssigkeit aufschwimmen,
wenn es unter den Flüssigkeitspiegel gedrückt wird. Diese Tatsache
ist das Grundprinzip vieler PM-Entwürfe. Was jedoch fast immer
übersehen wird, ist die Tatsache, daß das aufschwimmende Objekt
kein Loch in der umgebenden Flüssigkeit hinterläßt, sondern
die Flüssigkeit nachströmt. Allgemein kann das so formuliert werden:
Dies hat einschneidende Bedeutung für die Energiebilanz. Man sollte sich insbesondere vergegenwärtigen, daß hier zwei Massen die Plätze tauschen und damit auch zwei Arbeiten in der Energiebilanz berücksichtigt werden müssen |
Ein paar Schlußfolgerungen können wir ziehen:
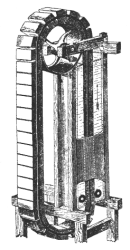
Ein klassischer Vorschlag zum Bau eines Perpetuum Mobile basiert auf einem schwimmfähigen, biegsamen und gut geschmierten Seil. Das Seil soll in einem asymmetrischen U-Rohr laufen. Auf der niedrigen Seite (links) ist eine Dichtung vorgesehen, die zwar das Seil hindurchgleiten läßt, aber das Ausdringen der Flüssigkeit verhindert. Die Idee ist klar. Der einseitige Auftrieb des Seiles im längeren Teil des Rohres soll zu einer immerwährenden Bewegung führen.
 |
Ord-Hume gibt in seinem Buch Perpetual Motion - The History of an Obsession folgende Erklärung, warum diese Apparatur nicht funktionieren kann: "Erneut versagt das System aufgrund der Anforderungen an Luft und Wasser in einer unrealistischen und praxisfernen Situation. Abgesehen von der Reibung in der Stützrolle, muß das gut geschmierte Seil durch eine wasserdichte Dichtung gezogen werden, die einen nennenswerten Druck auf das Seil ausüben muß, um die Flüssigkeit im Rohr zurückzuhalten.Versucht man, mehr "Kraft" auf der hebenden Seite des Rohres zu erzielen, indem man das Rohr verlängert, dann wird auch das Gewicht des Wassers erhöht, die Tendenz zur Leckage zwischen Seil und Dichtung steigt und deswegen muß die Dichtung das Seil nur noch fester umschließen. Als wäre das nicht genug, auch die Reibung durch Biegen und Glätten des geschmierten Seiles im Wasser ist beachtlich. Der Wirkungsgrad dieser Maschine läge beträchtlich unter 1, und erinnern Sie sich, daß endlose Bewegung nur bestehen kann, wenn der Wirkungsgrad über 1 liegt."1(S. 108, Übers. Gramatke) |
Klingt einsichtig, stimmt aber nicht. Ord-Hume argumentiert mit Reibung.
Aber selbst wenn keine Reibung vorhanden wäre, könnte diese Apparatur
nicht funktionieren.
Der Erfinder des Gerätes weckt mit seiner Zeichnung Erwartungen, die
in der Praxis nicht zutreffen. Haben Sie jemals ein schwimmendes Seil beobachtet?
Wenn ja, kann die Zeichnung stimmen? Wenn das Seil schwimmfähig ist,
warum schwimmt es dann nicht im unteren Teil des U-Rohres?
 |
 |
 |
||
| So verhält sich ein steifes Seil |
Ein flexibles Seil schwimmt etwa so... |
...außer es wird straff gespannt. |
 |
Immer noch ist unklar, warum dieses Prinzip nicht funktioniert. Hier
eine ganz einfache Erklärung:
|
 |
Es gibt Erfinder, denen klar ist, daß die vorhin beschriebene Apparatur
mit dem schwimmfähigen Seil nicht funktionieren kann. Eine Kette, an
der leichte Schwimmer befestigt sind, kann dem Hauptmangel entgegenwirken,
denn an den Auftriebskörpern kann die Druckkraft des Wassers von oben
und unten angreifen. Dieses Beispiel wurde von Mr. Frank Tatay erdacht, der
1929 das US-Patent Nr. 1,708,807 dafür erhielt. Die
Auftriebskörper erzeugen eine nach oben gerichtete Kraft, die primär
von der Dichte und Größe der Schwimmer sowie der Höhe der
Flüssigkeitssäule abhängt. Damit sollte es möglich sein,
einen einzelnen Auftriebskörper gegen den Flüssigkeitsdruck durch
die Dichtung im Boden des Tanks zu ziehen.
Das klingt zu schön, um wahr zu sein. Das Geheimnis liegt - in den Zwischenräumen zwischen den Schwimmern! |
|
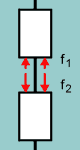 |
Ein näherer Blick zeigt, daß die Kraft f1, die am Boden des oberen Schwimmers angreift, geringer sein muß als f2, die auf den unteren Schwimmer wirkt. Die resultierende Kraft zeigt folglich nach unten, was eher nicht im Sinne des Erfinders ist. Man kann diese Betrachtung für alle benachbarten Schwimmer wiederholen, mit dem Ergebnis, daß wir eine abwärts gerichtete Kraft beobachten. Mit einer Ausnahme... |
Zugunsten des Erfinders nehmen wir an, daß der Zwischenraum zwischen
den Schwimmern gering ist, so daß die Differenz
f2-f1nahezu Null wird. Ignorieren wir auch die Summe
dieser geringen Kräfte und fragen uns: wird unter diesen Bedingungen
die Maschine arbeiten?
Zwischenbilanz. Die summierten Auftriebskräfte aller oberen Schwimmer
sind höchstens so groß, wie die Auftriebskraft eines einzigen
hohen Schwimmers mit derselben Querschnittsfläche.
Bis jetzt haben wir den untersten Schwimmer nicht betrachtet. Wir können nochmals dasselbe Diagramm anwenden, wie vorhin. Nun wird klar, daß die abwärts wirkende Kraft, die den untersten, teilweise im Tank befindlichen Schwimmer herauszudrücken versucht, größer ist, als die summierte Auftriebskraft aller oberen Schwimmer.
Anders ausgedrückt: Die Maschine liefe genau in der umgekehrten Richtung als erwartet! Wenngleich der Gedanke des Erfinders nicht zutrifft, freuen wir uns dennoch; schließlich ist es egal, in welche Richtung die Maschine läuft, Hauptsache, sie ist ein Perpetuum Mobile!
Jetzt habe ich Sie gehörig auf's Glatteis geführt! Wo ist der Fehler?
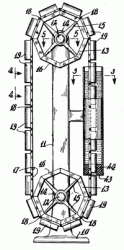
Wir haben die einfachen Perpetua Mobilia, bestehend aus Kette und Schwimmer, eingehend untersucht. Gelegentlich werden Auftriebsmaschinen konstruiert, die erkennen lassen, daß der Erfinder ähnliche Gedankengänge hatte und die grundlegenden Fehler vermeiden wollte. Ein raffiniertes Prinzip ist die Verwendung von Auftriebskörpern, die zeitweise von der umlaufenden Kette abgekoppelt werden. 1974 ließ Ralph W. Gilmore mit dem US-Patent Nr. 3,857,242 eine solche Apparatur patentieren.
| ***image*** |
Dieser Entwurf vermeidet den Hauptmangel der vorigen Maschinen. Hier werden die Auftriebskörper in Bodennähe des Tanks waagerecht durch eine Dichtung geführt. Da die Körper zylindrische Form haben, wirkt die Druckkraft, die den Schwimmer aus dem Tank treiben will, nur auf die Stirnfläche. Wir treffen folgende Annahmen:
Die Annahmen sind unter dem technischen Aspekt praxisfremd, aber zugunsten des Erfinders. Können Sie herausfinden, ob Mr. Gilmores Maschine funktionsfähig ist? Und wenn sie es nicht ist, warum?2
Ich möchte nochmals hervorheben, daß ich ohne Not keine Formeln benutzen will, abgesehen von ein paar einfachen Additionen. Der Hauptfehler einer Idee muß so gut herausgearbeitet werden, daß sich der Gebrauch der Mathematik erübrigt. Wir schauen uns hier die zweite Klasse der Auftriebsmaschinen an, die etwas schwieriger zu verstehen sind. Zu Ihrer Bequemlichkeit und zum Vorteil des Erfinders wollen wir wie üblich Reibungsverluste und die geringe Kompressibilität der Flüssigkeit nicht berücksichtigen.
| ***image*** | Diese Art von Maschinen wurde dutzendemale patentiert. Eine kleine Liste
von neuen Beispielen:
Das Prinzip ist einfach. Der Mechanismus ist vollkommen eingetaucht. An einer Kette ist eine Anzahl Auftriebselemente befestigt. Die Auftriebskörper haben einen inneren Mechanismus, der bevorzugt durch die Schwerkraft betätigt wird. Auf der einen Seite der Kette haben die Körper großes Volumen und sind schwimmfähig. Auf der anderen Seite der Kette wird ihr Volumen so verringert, daß sie absinken. Auftrieb auf der einen Seite der Kette, Schwerkraft auf der anderen - das ergibt endlose Bewegung mit Kraftüberschuß! Gelegentlich werden gegenüberliegende Auftriebskörper noch durch Schläuche verbunden, um den erwarteten Effekt zu verstärken. |
Einsichtig, daß die Anzahl der Schwimmer nahezu beliebig sein kann. Wir vereinfachen die Maschine und betrachten den Weg eines einzelnen Auftriebskörpers.
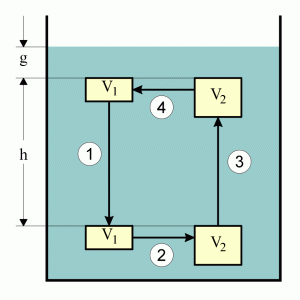 |
Angenommen, der Schwimmer bewegt sich gegen den Uhrzeigersinn. Die einzelnen
Volumina bewirken unterschiedliches Auftriebsverhalten::
Die Masse des Auftriebskörpers und die Volumina V1 and V2 werden geeignet gewählt. Wir erwarten eine Art Kreisprozeß:
|
Wenn wir annehmen, daß der Mechanismus im Inneren des Auftriebselements bei seiner Rundreise verlustfrei arbeitet, dann addieren sich die beiden Änderungen des Volumens in der Energiebilanz zu Null. Da nun die Schritte 1 und 3 echte Gewichts- bzw. Auftriebskräfte erzeugen, sollte die Maschine einen beachtlichen Energieüberschuß produzieren. Das ist ein attraktiver Einfall, der wie bereits erwähnt, viele Male gedacht wurde.
Bevor Sie sich nun aufmachen, ein solches echtes Perpetuum Mobile zu bauen, bitte ich Sie freundlich, bis zum Ende dieses Abschnittes weiterzulesen, denn Sie haben jetzt eine gute Gelegenheit, Enttäuschungen aus dem Weg zu gehen. Wir wollen den "Kreisprozeß" genau analysieren. Da müßte man doch herausfinden, in welchem Schritt der "magische" Teil der Energieerzeugung stattfindet.
Alle mir bisher bekannten Entwürfe dieser Auftriebsmaschinen gehen davon aus, daß die Auftriebselemente einen geschlossenen Weg zurücklegen. Dabei haben sie, wenn sie an ihrem Ausgangspunkt ankommen, wieder ihre ursprüngliche Orientierung und ihr ursprüngliches Volumen. Nachdem wir im Augenblick die umgebende Flüssigkeit nicht betrachten wollen, sondern uns nur auf den Schwimmer konzentrieren, stellen wir fest, daß sein Weg dem ersten Hauptsatz der Thermodynamik genügt. In unserem Fall können wir ihn so fassen:
Das erste Ergebnis ist garnicht so schlecht. Folglich kann die Wahl des Weges nicht die Ursache der perpetuierlichen Eigenschaft sein. Und tatsächlich: alle diese Konzepte behaupten, daß Auftriebs- bzw. Gravitationskraft die Quelle der Energie sind.
Zunächst untersuchen wir die beiden senkrechten Bewegungen 1 und 3. Wir rekapitulieren, wie Auftrieb zustande kommt: die Kraft, die auf das eingetauchte Objekt wirkt, entsteht durch den Unterschied der Druckkräfte auf Ober- und Unterseite des Objektes. Wenn ein Objekt absinkt oder aufsteigt, wird das entsprechende Flüssigkeitsvolumen an den Ausgangsort des Körpers transportiert.
|
|
| Schritt 1: Das Objekt sinkt. Damit bewegt sich dasselbe Volumen Flüssigkeit V1 nach oben. | Schritt 3: Das Objekt steigt auf. Das äquivalente Flüssigkeitsvolumen V2 bewegt sich nach unten. |
Schlußfolgerung: Insgesamt hat sich das Differenzvolumen V2-V1 an Flüssigkeit nach unten bewegt, während das eingetauchte Objekt zum Ausgangspunkt zurückgekehrt ist. Wir haben Masse bewegt, ohne Energie zu investieren und damit auch die Quelle der perpetuierlichen Bewegung ermittelt! Wirklich?
Bisher haben wir in unserer Untersuchung die Schritte 2 und 4 außer Acht gelassen, was auch viele Erfinder gerne machen. Verwenden wir dieselbe Methode wie bei den vorigen Schritten 1 und 3.
|
|
| Schritt 2: Das Flüssigkeitsvolumen V2-V1 wird nach oben bewegt | Schritt 4: Das Flüssigkeitsvolumen V2-V1 bewgt sich nach unten |
Ein voreiliger Schluß wäre, daß die sich die Auf- und Abwärtsbewegungen des konstanten Flüssigkeitsvolumens aufheben. Das Ergebnis des vorigen Analyseschrittes bleibe unangetastet und die Maschine weiterhin perpetuierlich. Doch langsam! Wir müssen schon etwas genauer hinsehen!
Wir haben die mechanische Arbeit ignoriert, die zum Verschieben der Flüssigkeit nötig ist. Betrachten wir den Flüssigkeitsanteil, der in Schritt 3 nach unten sinkt. Er besteht aus den Volumina V2-V1 and V1. Man sieht leicht, das der Anteil aus V1 genau denselben Anteil aus Schritt 1 ausgleicht. Konzentrieren wir uns folglich auf den Anteil V2-V1.
Wir haben die Flüssigkeitsmasse, die dem Volumen V2-V1 entspricht, um die Höhe h+g gehoben, und anschließend um h und g nach unten bewegt. Die Gesamtenergiebilanz ist Null. Was lernen wir aus dieser länglichen Analyse? Der Schlüssel zum Verständnis, warum das Konzept untauglich ist, liegt in den Schritten 2 und 4, die gerne nicht berücksichtigt werden, da sie im Verhältnis zur beliebigen Höhe der Maschine vernachlässigbar erscheinen.
Erinnern Sie sich an den ersten Hauptsatz der Thermodynamik? Erinnern Sie sich an die Fassung, die ein bißchen weiter oben schon zu lesen war:
Welche Massen sind an diesem Kreisprozeß beteiligt?
Energiemengen der Größe Null können wir addieren, so oft wir wollen, positiv kann die Bilanz nicht werden. Selbst wenn wir die diskutierte Maschine anfänglich in Bewegung versetzen, wird sie durch die bislang nicht berücksichtigten Reibungsverluste bald zum Stillstand gebracht.
Es ist schwierig, diesen Maschinentyp einer der beiden Kategorien zuzuordnen, denn sie enthält wesentliche konstruktive Merkmale beider Grundideen. Das nächste Beispiel stammt von einem unbekannten Erfinder aus der Zeit um 1925. Es sei stellvertretend für viele andere Konstruktionen des gleichen Prinzips analysiert.
|
Eine Kette wird durch die Gewichtskraft der schwimmfähigen Kugeln angetrieben. Die Kugeln steigen in einem wassergefüllten Schacht auf. Mittels zweier Schieber, die verlustfrei arbeiten sollen, wird der Weg für die Kugeln freigegeben und gleichzeitig das Ausrinnen des Wassers verhindert. |
Ein Haufen Ideen und viel Technik für ein Prinzip, das bereits mit einer einzigen Kugel nicht funktionieren kann. Der Erfinder bedachte nicht, daß jede Kugel, die aufsteigt, dieselbe Menge Wasser nach unten verdrängt. Die Maschine versagt folglich bereits nach kurzem Betrieb durch Wasserverlust. Aber leistet sie dennoch nicht mehr Arbeit, als der Auftriebsweg der einzelnen Kugel nach oben? Eine kleine Energiebilanz ist schnell aufgestellt. Beachten Sie bitte, daß hier keine Annahmen über Dichte der Kugel und des Wassers gemacht werden müssen, außer daß die Kugel schwimmfähig ist. Das Volumen der Kugel ist ebenfalls ohne Bedeutung.
Es soll gelten:
Positive Vorzeichen vor einer Teilenergiebilanz bedeuten Arbeit, die in das System in Form von potentieller Energie gewinnt; negative Werte sind Arbeit, die das System abgibt. Die Bilanz des Aufschwimmens einer Kugel sieht dann so aus:

Die Gesamtenergie ist damit:
| E = E1 + E2 + E3 + E4 = (-M + m) g h2 + (-M + m) g h + (-M + m) g h1 - m g (h1 + h2 + h) = (-M + m - m) g h + (-M + m - m) g h1 + (-M + m - m) g h2 = -M g (h + h1 + h2) |
Die Energiebilanz verzeichnet im günstigsten Fall nur den Verlust
(M - m) g (h + h1 + h2).
Dieses Ergebnis entspricht der offensichtlichen Tatsache, daß die Kugel
auf ihrem geschlossenen Weg die nutzbringende Arbeit
m g (h + h1 + h2) leistet,
während die Flüssigkeitsmasse M, die dem Volumen der Kugel
äquivalent ist, sich um die Gesamthöhe des Wasserspiegels nach
unten verlagert hat.
In der Praxis entstehen weitere Verluste durch die Flüssigkeitsreibung
und andere Effekte. So kann man ganz gewiß kein Perpetuum Mobile bauen.
Kritische Leser, die aufgepaßt haben, werden Einwände vorbringen. Einwände, die jedem zünftigen PM-Konstrukteur bekannt sind, und die Anlaß für noch ineffizientere Apparaturen waren.
| Einwand 1: | Die Maschine könnte so ausgelegt werden, daß die Kugel auch beim Aufschwimmen Arbeit leistet, indem sie ein vergleichbares Antriebsband betätigt. Damit ließe sich eine erheblich bessere Ausnutzung der Arbeit erreichen. Einmal Weg nach oben, einmal nach unten, das ergibt einen Wirkungsgrand von fast 200%! | |||
|---|---|---|---|---|
|
|
|
|||
| Antwort 1: | Das mit dem Wirkungsgrad ist nicht schlüssig. Es sollte nicht vergessen
werden, daß die Kugel schwimmfähig ist. Die Auftriebskraft ergibt
sich damit zu (M - m) g. Folglich ist die Arbeit, die die
Kugel beim Aufstieg leistet: E6 = -(M - m) g (h + h1 + h2)
Beim Herunterfallen leistet die Kugel die Arbeit
Addiert man diese beiden Arbeiten zusammen, ergibt sich: Das ist das beste Ergebnis, das erzielbar ist und entspricht exakt der Arbeit, die unter idealen Bedingungen das nach unten bewegte Wasser zu leisten vermag! Doch dazu ist die Kugel unnötig; eine gewöhnliche Wasserkraftmaschine täte es auch. |
|||
|
|
|
|||
| Einwand 2: | Die Bewegung der Masse M wurde als Verlust gebucht. Schließlich könnte man sich ja eine Art Wasserkraftmaschine vorstellen, die diese Energie nutzbringend aus dem System entnimmt. | |||
|
|
|
|||
| Antwort 2: | Das ist richtig, war jedoch in der Analyse der Maschine nicht gefragt,
da der Erfinder auf dieses Detail verzichtet hat. Dennoch ist es sinnvoll,
den Punkt zu betrachten. Tatsächlich haben wir unter dem obigen
Punkt 1 dieses Szenario bereits durchgespielt! Die Kugel, deren Arbeit
optimal genutzt wird, entspricht dieser Wasserkraftmaschine. Es könnte
daran gedacht werden, die Arbeit, die die Kugel beim Aufstieg leistet und
die Arbeit, die das Wasser beim Weg nach unten leistet, nutzbringend zu gewinnen.
Das klingt plausibel und sollte analysiert werden. Lassen wir die technischen
Schwierigkeiten, die die Praxis böte, beiseite. Dann kann man sich den
Weg der Kugel in einem Paar konzentrischer Rohre vorstellen, von denen in
geeigneter Weise die Arbeit abgeführt wird.
|
|||
Die eben analysierte Maschine ist in dieser Beziehung eine denkbar ungünstige Lösung, denn ihr Funktionsprinzip verlangt durch die Auftriebsbedingung m < M eine schlechtere Ausnutzung der gewinnbaren Leistung als mit einer konventionellen Wasserkraftmaschine möglich wäre.
Wenn Sie eine detailliertere Diskussion der Physik funktionsunfähiger Auftriebsmaschinen lesen wollen, schauen Sie zu Donald Simaneks Seite über fehlgeleitete Auftriebsideen. Sollten Ihnen Parallelen zwischen unseren Gedankengängen auffallen, werten Sie das bitte nicht als Beweis für die Große Verschwörung, sondern eher für wissenschaftlichen Austausch und gleiches Verständnis elementarphysikalischer Tatsachen.
2. Nein, schicken Sie mir keine Lösung! Sparen Sie sich die Arbeit; ich weiß, warum dieser Apparat untauglich ist.
| Stand: 23.02.2004 / |
|