 |
 |
Seit Jahrtausenden sind schiefe Ebenen ein weit verbreitetes mechanisches Hilfsmittel. Schon früh fand man heraus, daß es weniger anstrengend ist, eine Last schräg aufwärts zu schleifen, als sie senkrecht hochzuheben. Obwohl dazu weniger Kraft benötigt wird, spart man nichts an Arbeit; im Gegenteil, durch die unvermeidliche Reibung benötigt man mehr Aufwand. Der genaue Zusammenhang zwischen Neigung der schiefen Ebene und der aufzuwendenden Kraft blieb bis in die Renaissance unklar. Erst die Künstler-Ingenieure und Mathematiker-Astronomen des fünfzehnten und sechzehnten Jahrhunderts führten detaillierte Analysen dieses scheinbar einfachen Konstruktionselementes durch. Bis zu jener Zeit - und manchmal auch heute noch - gibt es lückenhafte Ansichten über schiefe Ebenen.
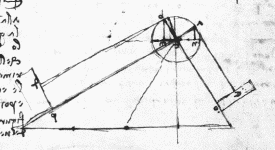
Es ist immer ein guter Gedanke, erst bei Leonardo da Vinci nachzuschlagen und zu prüfen, ob Leonardo nicht Einsichten in ein bestimmtes Phänomen hatte. Tatsächlich sind von ihm Zeichnungen überliefert, die denen Stevins frappant ähnlich sind. In Leonardos Notizbuch Sul volo degli uccelli (Über den Flug der Vögel) finden sich diese bemerkenswerten Skizzen.
 |
 |
Leonardo kam mit seinen Überlegungen zu einer brauchbaren Theorie der wirkenden Kräfte - 130 Jahre vor Simon Stevin.
Simon Stevins (1548-1620) Untersuchung über die schiefe Ebene gilt als
erster Meilenstein auf dem Weg zum modernen Energieprinzip. Stevin wählte
als Modell eine Ebene mit zwei verschiedenen Steigungen und eine endlosen
Kette. Doch hatte Stevin tatsächlich den Beweis der Unmöglichkeit
eines Perpetuum Mobile im Sinn?
Sein Gedankengang soll kurz dargestellt werden.
|
|
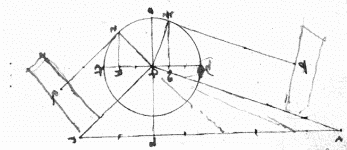
Stevins schiefe Ebene |
Ein geteiltes System |
Der Ausgangspunkt von Stevins Überlegung sind einige Grundannahmen:
Annahmen sind vollkomen legitim, wenn es darum geht, eine neue Theorie zu entwickeln. Ebenso hätten andere Annahmen als Axiome dienen können, aber Stevin entschloß sich für diese, nicht zuletzt wohl deshalb, weil sie einfach und plausibel sind - ein Motiv, das später von Galileo Galilei zum Teil der Methode erhoben wurde.
Aus der Symmetrie konnte Stevin schließen, daß rechts und links an der Kette die Kraft f1 angreift. Für die weitere Betrachtung ist deshalb der untere, bogenförmige Teil der Kette verzichtbar. Die beiden Kräfte f2 und f3 müssen für sich allein das Gleichgewicht der Kette bewirken, folglich gleich sein. Damit läßt sich ermitteln, wie die Neigung der Ebene die an einer Masse angreifende Kraft beeinflußt.
***Bild***
Die Massen der Teilketten sind als Einzelmassen
zusammengefaßt und idealisiert
Dies deckt sich mit der modernen Auffasung des Superpositionsprinzips, das davon ausgeht, daß Kräfte vektoriell addiert werden können und daß für einen Körper im statischen Gleichgewicht die vektorielle Summe aller an ihm angreifenden Kräfte Null sein muß.
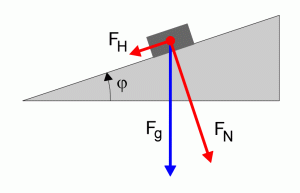
Vektorielle Addition der Kräfte
Wie die vektorielle Betrachtung der Kräfte zeigt, resultieren aus der senkrecht nach unten wirkenden Gewichtskraft Fg des Körpers
Es gilt:
Was bleibt als Fazit? Stevin kam zu einer Theorie der Kräfte, die auf Körper wirken, wenn sie auf eine schiefen Ebene liegen. Doch Stevin bewies nicht die Unmöglichkeit eines Perpetuum Mobile, sondern er nahm sie als Axiom an, um seine Theorie zu entwickeln.
Stevin ging bei seinen Betrachtungen von Kräften an der schiefen Ebene von einem System im Gleichgewicht aus. Galileo Galilei (15.2.1564 - 8.1.1642) führte eine dynamische Sichtweise ein, um Schlüsse über die beschleunigte Bewegung von frei fallenden Körpern zu verifizieren.
 |
Sehen wir uns die Methode an, mit der Galileo Galilei untersuchte, wie
Objekte fallen! Er bekennt freimütig, daß er kein brauchbares
Meßverfahren hatte, um die kurzen Zeitintervalle ausreichend genau
zu messen. Er mußte folglich den Vorgang so verlangsamen, daß
er für seine Meßmethoden zugänglich war. Man könnte
sich z.B. vorstellen, ein Objekt in einer dichten Flüssigkeit absinken
zu lassen. Doch in Wasser oder gar Honig wird ein sinkendes Objekt
frühzeitig eine konstante Geschwindigkeit erreichen, die aus dem
Gleichgewicht der Flüssigkeitsreibung und der auf das Objekt wirkenden
Abtriebskraft bestimmt wird1. Um die
charakteristische Eigenart der Bewegung zu erhalten, und eine Art "Zeitlupe"
zu erzielen, baute Galileo eine Rampe, auf der er Kugeln herabrollen
ließ. Er beschreibt seine Methode so: |
| "Bei der Untersuchung der natürlichen beschleunigten Bewegung
ließen wir uns von den Gewohnheiten der Natur selbst leiten, die uns
in all ihren verschiedenen Prozessen lehrt, nur die allgemeinsten, einfachsten
und leichtesten Mittel anzuwenden" (Kuhn,
Physik III B, Mechanik, S.94)
"Ich habe auf die folgende Weise versucht, mir Gewißheit zu verschaffen (über) die Beschleunigung, wie sie tatsächlich bei fallenden Körpern auftritt. [...] Zuerst wurde ein Brett oder Balken aus Holz ausgesucht, ungefähr zwölf Ellen lang, eine halbe Elle breit und drei Fingerbreit dick; sodann wurde in die Oberseite eine Rinne von wenig mehr als einem Finger Durchmesser gegraben; nachdem wir diese Hohlrinne ganz gerade gezogen und glatt poliert und sie mit Pergament ausgelegt hatten, das gleichfalls so glatt und poliert wie möglich war, ließen wir in ihr eine feste, glatte und vollkommen runde Bronzekugel rollen. Nachdem wir das Brett in eine abfallende Lage gebracht hatten, [...] ließen wir die Kugel die Rinne entlangrollen und maßen dabei [...] die Zeit, die sie zum Hinabrollen brauchte. Dieses Experiment wiederholten wir mehrere Male, um die Zeit so genau zu messen, daß die Abweichung zwischen zwei Beobachtunngen nie mehr als das Zehntel eines Pulsschlages betrug. Nachdem wir diese Operation ausgeführt und uns von ihrer Zuverlässigkeit überzeugt hatten, ließen wir beim nächsten Mal die Kugel nur ein Viertel der Länge der Rinne hinabrollen; und als wir dann die Zeit für das Hinabrollen maßen, sahen wir, daß sie genau die Hälfte der zuvor gemessenen betrug. Sodann machten wir den Versuch mit andren Entfernungen, wobei wir die Zeit für die ganze Länge mit der für die Hälfte, mit der für zwei Drittel, für drei Viertel, kurz für alle möglichen Bruchteile der Länge der Rinne vergleichen; und bei all diesen Experimenten, die wir wohl hundert Mal und öfter wiederholten, stellten wir fest, daß die die zurückgelegten Strecken sich zueinander verhielten wie die Quadrate der betreffenden Zeiten, und dies traf zu für jedes Gefälle der Ebene, d.h. der Rinne, in der wir die Kugel entlangrollen ließen. Wir stellten auch fest, daß die Zeiten für das Hinabrollen bei verschiedenem Gefälle in einem Verhältnis zueinander standen, das [...] der Experimentator vorausgesagt und demonstriert hatte." (Kearney, Und es entstand ein neues Weltbild, S. 68f.) |
Einige Punkte, wie Galileo seine Aufgabe bearbeitete, seien hier hervorgehoben:
Diese von Galileo Galilei entwickelte Synthese aus Theorie und Experiment gilt heute noch als vorbildliche wissenschaftliche Arbeitsweise. Diese Methodik sei all' jenen ans Herz gelegt, die ein Perpetuum Mobile erfinden und den ersten theoretischen Schritt nur zum Teil gehen. Die mathematische Handwerksarbeit nach der spekulativen Phase wird gerne beiseitegelassen, und auf das Experiment nebst Verifikation oder Falsifikation der Theorie verzichtet.
Die Theorie der Kräfte, die auf Massen auf einer schiefen Ebene wirken und die Theorie des freien Falles waren Mitte des siebzehnten Jahrhunderts durchentwickelt und gesichert. Das hinderte hoffnungsvolle Erfinder nicht daran, perpetuierliche Maschinen zu erdenken, die sich der schiefen Ebene bedienten, um einen vermeintlichen Vorteil aus den Hangabtriebskräften zu ziehen. Häufig wird ein arabisches Rad auf diese Art "verbessert". Leitschienen sollen den Umlauf der Kugeln so strecken, daß die wirksamen Drehmomente an den Hebeln vergrößert werden.
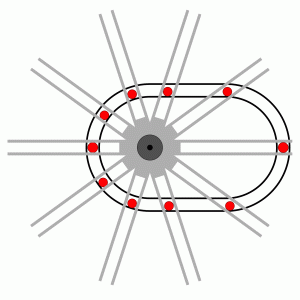
Die längeren Hebelarme sollen eine bessere
Wirkung erzielen, als beim einfachen arabischen Rad
Der Ansatz ist naheliegend und wurde mehrfach veröffentlicht. In einem Internet-Forumsbetrag las ich dazu den Kommentar: "Ich sehe keinen Grund, warum diese Idee nicht funktionieren soll" - ich hingegen sehen keinen Grund, warum sie es sollte. Da die Funktionsweise des Mechanismus offenbar unabhängig von der Anzahl der Arme und umlaufenden Kugeln ist, kann die Analyse anhand eines Hebels und einem Paar Kugeln beginnen. Wird diese Bewegung in mehrere Schritte zerlegt, dann ist der nicht behebbare Mangel der Konstruktion leicht zu erkennen:
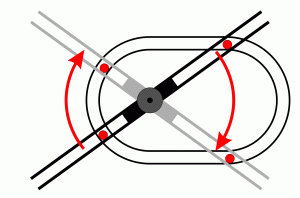 |
So bewegt sich der Hebel nicht! Trotz der längeren Hebelarme auf der rechten Seite ist das wirksame Drehmoment links größer. Der Grund ist in der Wirkung der schiefen Ebene (hier ist sie!) begründet, die die Kreisbogensegmente an der Kontaktstelle lokal darstellen. |
| Um die linke Kugel anzuheben, muß auf der rechten Seite mehr Drehmoment aufgebracht werden, als die Schwerkraftwirkung allein erbringt. | |
| In einem begrenzten Bereich bewegt sich die rechte Kugel durch ihr Eigengewicht von oben nach unten. Sie hebt dabei die linke Kugel um einen entsprechenden Bruchteil. Die Schwerkraft wirkt hier als Antrieb. In der Praxis ergäben sich auch hier Verluste, da die Kräfte auf die gekrümmten Schienen den gleichen Gesetzmäßigkeiten unterliegen wie die an einer schiefen Ebene | |
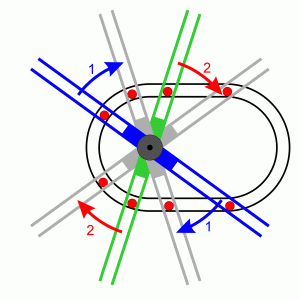 |
Bleibt die Frage: Mit welcher Energie werden die Bahnabschnitte 1 und
2 durchlaufen? Auf der linken Seite muß die Kugel angehoben werden,
ohne daß eine geeignete Kraftquelle auf der rechten Seite zur
Verfügung steht, denn hier bewegt sich die gegenüberliegende Kugel
in der waagerechten Schiene. Die Klemmwirkung, die in der Praxis aufträte,
täte ein Übriges.
Nun ist der Punkt erreicht, an dem die anderen Hebel des Apparates benötigt werden, denn sie könnten die notwendige Arbeit beim Durchlaufen der hier betrachteten Teilstücke leisten. Doch wie kommt man zu einer sinnvollen Aussage, wenn die Anzahl der Hebel beliebig sein soll? |
| Eine sinnvolle Betrachtung kann z.B. dadurch erfolgen, daß beide Bögen mit einer Art homogenem flexiblen Schnur gefüllt sind. Eine Betrachtung dieses Falles ist zwar mathematisch möglich, doch schwierig. Ist sie zu diesem Zeitpunkt nötig? | |
| Da wir wissen, daß die beiden waagerechten Schienen im Sinne der Energiebilanz keinen Beitag leisten, kann ein flexibles Band ohne irgendwelche Hebel ebenso als Modell dienen. Und auf einmal ist sonnenklar: so kann es nicht funktionieren! | |
| Die ganze Betrachtung läßt sich deutlich vereinfachen, wenn man sich überlegt, daß jede einzelne Kugel auf einer geschlossenen Bahn an den Ausgangspunkt zurückkehrt. Die Energiebilanz für diesen Umlauf ist im Idealfall neutral, niemals aber positiv. |
Diese Idee wurde in der Geschichte des Perpetuum Mobiles einige Male in Varianten publiziert. Das nachstehende Patent BExxx von yyy schließt den vordergründigen Mangel der Klemmwirkung aus der vorigen Analyse aus. Für diesen Vorteil muß jedoch ein anderer Nachteil in Kauf genommen werden. Sie wissen inzwischen genug, um das selbst herauszufinden.
***image***
Belgisches Patent Nr. yyy.
Andere Enwürfe gehen davon aus, daß an einer schiefen Ebene nicht nur die Hangabtriebskraft wirkt, sondern auch im Newtonschen Sinne Gegenkräfte auf die Unterlage. Diese Gegenkräfte lassen sich in zwei Komponenten zerlegen, von denen eine die schiefe Ebene auf die Unterlage preßt, die andere die Ebene beiseite drückt. In der Technik werden solche Mechanismen als "Schubkeilgetriebe" bezeichnet und verwendet. Alois Drasch wollte 1868 diese Kraft in einem rotierenden "Motor" nutzen, in dem eine schwere Kugel perpetuierlich in einem zylindrischen Trog abwärts rollen sollte.
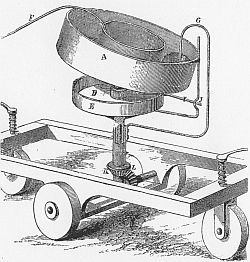
Draschs Motor mit kontinuierlicher Verstellung der
Abgabeleistung. Der Hebel F sollte dem Fahrer des
Vehikels ermöglichen, den Trog je nach Bedarf zu kippen.
Daul, Das Perpetuum Mobile, S.112
Obwohl Drasch auf diese Maschine zum Antrieb eines Fahrzeuges ein US-Patent erhielt, konnte sich die Erfindung nicht durchsetzen, basiert sie doch auf demselben Prinzip wie dieses Fahrrad, das Muskelkraft spart, indem es beständig hangabwärts fährt.
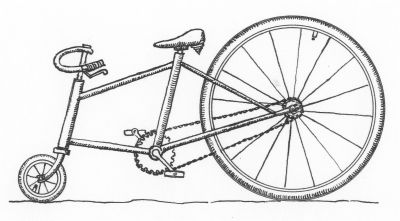
HP Gramatkes Abwärtsfahrrad für Fans der Freien Energie.
Die Pedale sind nur bei besonders steilen Bergauffahrten nötig.
Anmerkungen:
1. Eine konstante Geschwindigkeit stellt sich auch beim freien Fall in der Luft ein, jedoch ist diese Situation für Laboratorien normaler Raumhöhe nicht relevant.
| Stand: 23.02.2004 / |
|