
Hebel im Gleichgewicht
F1 ´ r1 = F2 ´ r2
Die Argumente angehender Perpetuum-Mobile-Bauer sind fast immer die gleichen. Typischerweise werden mechanische Gesetzmäßigkeiten nicht oder nur zum Teil verstanden. Hier ein Paar Tips zum "Zerlegen" von Perpetuum Mobiles. Um's nicht zu kompliziert zu machen, gibt es physikalisch-mathematische Schonkost in kleinen Häppchen.
Verwirrung pur! Manchmal habe ich den Eindruck, daß unter dem Wirkungsgrad jeder Perpetuum-Mobile-(Webseiten-)Autor etwas anderes versteht. Mit ein paar einfachen Definitionen läßt sich die Verwirrnis beheben:
| Definition: | Der Wirkungsgrad ist das Verhältnis der abgegebenen
zur aufgenommenen Leistung. Anders ausgedrückt: Hier wird das System
gesamthaft betrachtet, mit allen zufließenden und nutzbar entnommenen
Leistungen. Ungenutzte Leistung, die z.B. in Form von Abwärme entweicht,
wird nicht im Wirkungsgrad aufgenommen.
Der Leistungsfaktor ist das Verhältnis der abgegebenen zur aufgewandten Leistung. |
|
|---|---|---|
|
|
|
|
| Bemerkungen 1: | Der Wirkungsgrad ist nach bisherigen Erkenntnissen und den Hauptsätzen
der Thermodynamik gemäß stets kleiner gleich 1. Der Leistungsfaktor ist eine Größe, vornehmlich von technischem Interesse ist, da er ein Maß für den Nutzen einer Maschine oder Einrichtung darstellt. Der Leistungsfaktor kann, wie im Falle der Wärmepumpe, deutlich über 1 liegen. Der Wirkungsgrad der Wärmepumpe ist dennoch kleiner 1. |
|
|
|
|
|
| Bemerkungen 2: | Im englischsprachigen Raum finden sich folgende Begriffe:
|
|
| Definition: | Die Abkürzung PM bedeutet "Perpetuum Mobile". | |
|---|---|---|
|
|
|
|
| Annahmen: | Es wird von folgenden Voraussetzungen ausgegangen:
|
|
Das klassische Perpetuum Mobile bedient sich eines radförmigen Mechanismus und unwuchtiger Massen. Die zugrundeliegende Idee für die Funktionsweise ist das Hebelgesetz.

Hebel im Gleichgewicht
F1 ´ r1 = F2 ´ r2
wobei das Einzel-Drehmoment M = F ´ r ist.
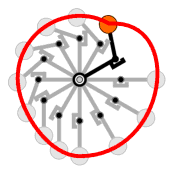
Damit der Hebel in Ruhe verharrt, gilt allgemein, daß die Summe aller Drehmomente = 0 sein muß. Falls die Summe der Drehmomente von 0 verschieden ist, beginnt der Hebel sich in Richtung des resultierenden Drehmomentes zu drehen. Betrachten wir einmal ein typisches Hebel-PM, auch arabisches PM genannt.
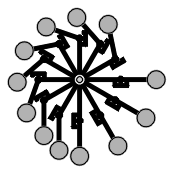
Hebel-Perpetuum Mobile
Dieses Maschinchen bleibt, kurz nachdem es angeworfen wurde, hin- und herschwankend stehen. Gilt hier das Hebelgesetz nicht? Es gilt. Der Erfinder hat einige wesentliche Aspekte übersehen:
 |
1. | Auf der linken Seite sind zwar die Hebel kürzer, aber die Anzahl
der Massen größer, so daß insgesamt die Momente ausgeglichen
werden können. Ich schreibe hier bewußt können, denn
es gibt viele Stellungen der Maschine, in der die Momente nicht ausgeglichen
sind. Bewegt man das Rad in eine dieser Positionen, so bewirkt das einseitige
Drehmoment, daß sich das Rad in einen Gleichgewichtszustand bewegt.
Könnten die Lagerreibung und andere Störeinflüsse ausgeschlossen
werden, würde der Mechanismus ewig oszillieren, genauso, wie er ewig
rotieren würde, wenn er mit genügend Schwung angeworfen wird. Im
Sinne der Definition ist das aber kein PM! In welche Richtung soll dieses Gerät bevorzugt laufen? Nach rechts, wegen der längeren Hebel? Oder nach links, wegen der größeren Anzahl Massen? |
|
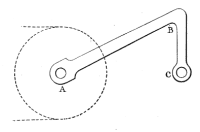 |
2. | Für das Drehmoment ist nicht der radiale Abstand der Masse zum Drehpunkt von Bedeutung, sondern ausschließlich der Abstand zwischen der senkrecht wirkenden Kraftlinie und dem Drehpunkt. Hier unterliegen viele Laien oft demselben Trugschluß wie der Konstrukteur dieser Fahrradtretkurbel um 1900. So ist bei senkrecht nach unten in C angreifender Kraft der wirksame Hebelarm der Abstand A-C und nicht A-B. | |
 |
3. | Der Energieerhaltungssatz gilt für die Massen in dieser Maschine.
Wenn man den Weg einer einzelnen Masse betrachtet, dann vollführt sie
einen zyklisch geschlossenen Weg. Und in seiner allgemeinen Form kann der
Energieerhaltungssatz in seiner Ausprägung als Potentialsatz so formuliert
werden: Wird ein Körper im Gravitationsfeld
auf einer geschlossenen Bahn zum Ausgangspunkt zurückbewegt, ist die
dafür aufgewendete Arbeit = 0. Anders ausgedrückt: die Arbeit, die durch die Bahn einer Masse auf der rechten Seite des Rades gewonnen wird, ist exakt die Arbeit, die notwendig ist, um dieselbe Masse wieder auf der linken Seite des Rades auf die ursprüngliche Höhe anzuheben. Die Anzahl der Arme, die Drehrichtung und die Momentangeschwindigkeit der Massen haben deshalb keinerlei Einfluß auf die (Nicht-)Funktionsweise! |
|
 |
PM, deren umlaufende Massen aus Kugeln oder einer bestimmten Menge Wasser bestehen, lassen sich mit dem Argument 3 aus der vorherigen Betrachtung widerlegen. Auch hier gilt der Energieerhaltungssatz für das umlaufende Medium, egal ob es sich dabei um eine Flüssigkeit handelt ,oder um Kugeln. Der Verlauf des Weges spielt bei der Betrachtung keine Rolle. |
Für Federelemente gilt im allgemeinen das Hookesche Gesetz, vorausgesetzt, das geeignete Material wird verwendet und der lineare Kraft-Weg-Bereich nicht verlassen. Bereits in der Schulphysik wird experimentell der folgende Zusammenhang erarbeitet:

Feder bei unterschiedlichen Lasten
Die Dehnung l der Feder hängt direkt proportional von der angreifenden Kraft F ab. Das Maß der Dehnung, die sog. Federkonstante D, vom Material und der Bauart der Feder. Der nachstehende Zusammenhang für die Federkonstante wird auch als Hookesches Gesetz bezeichnet:
D = DF / Dl = const
Eine Feder kann Energie speichern, weswegen sie in der Technik vielfältige
Anwendung findet. Federn haben stets eine von 0 verschiedene, positive
Federkonstante. Natürlich ist nicht jedes Material ein Hookesches Material;
Federkennlinien können je nach Dehnung unterschiedlich sein.
Jüngst ist mir eine Feder mit negativer Kennlinie vorgeschlagen worden.
"es muß eben eine Feder sein, die bei Weg an Zugkraft verliert." Was
ist davon zu halten? Im Vertrauen gesagt: Die Federn in meiner Bastelkiste
verhalten sich so nicht. Das hindert uns aber nicht daran, eine solche Feder
theoretisch zu analysieren.

Eine umgekehrt-hookesche Feder
Die Feder ist bei geringer Last lang, bei hoher Last kurz, die Federspannung
verhält sich genau umgekehrt wie bei einer hookeschen Feder. Den Fall
ohne Last vermag ich nicht einzuschätzen, die Feder würde vermutlich
maximale Länge haben (aber kaum unendlich).
Wir sollten bedenken, daß in jedem System im Gleichgewicht der alte
Satz actio gleich reactio gilt. Die Gegenkraft, die die Feder aufbringt,
ist genauso groß, wie die von der Last erzeugte Kraft. Mit einer solchen
Feder könnte man eine hübsche Maschine bauen:

Wassermaschine mit umgekehrt-hookescher Zugfeder 1
und hookescher Druckfeder 2, die das Ventil betätigt
Die Funktionsweise ist schnell erklärt. Wir beginnen mit einem leichten, also leeren Eimer. Die Feder 1 ist gedehnt, der Eimer betätigt durch sein Eigengewicht ein Ventil und wird aus dem Wasserreservoir gefüllt , wodurch er schwerer wird. Weil der Eimer schwer ist, zieht sich die Feder 1 zusammen und befördert den Eimer nach oben. An der oberen Rinne wird der Eimer durch einen Kippmechanismus geleert und damit wieder leicht. Das Spiel kann sich von vorne wiederholen. Das in die obere Rinne beförderte Wasser dient zum Antrieb einer Kraftmaschine.
Fazit: das ist ein PM, das offenkundig den Satz über die Erhaltung der
Energie verletzt (siehe oben). Das Potential, das
der gefüllte Eimer am oberen Punkt hat, ist höher, als das des
gefüllten Eimers unmittelbar nach dem Füllen. Die Feder verrichtet
also Hubarbeit. Aus welcher Kraftquelle speist sich die Feder?
Am Besten, wir vergessen das Ganze und bleiben bei den üblichen Federn.
Ein paar typische Einwände hört man immer wieder.
| Einwand 1: | Es gibt doch Materialien, wie z.B. Blei, die sich bei zunehmender Streckung mit immer weniger Kraft immer weiter dehnen lassen! | |
|---|---|---|
| Antwort: | Stimmt. Es handelt sich bei Blei oder bei Plastilin um (nahezu)
vollständig plastisch deformierbare Materialien, bei denen die gesamte
Arbeit, die man zum Strecken aufbringt, durch innere Reibung in Wärme
umgesetzt wird. Eine Federwirkung - und damit Energiespeicherung - ist nur
bei sehr begrenzten Wegen vorhanden. Man lasse sich aber durch die abnehmende Gesamtkraft nicht täuschen, denn wichtig für die Betrachtung ist die Kraft pro Querschnittsfläche, die aufgebracht werden muß. Und die nimmt bis kurz vor dem Bruch geringfügig zu. |
|
|
|
|
|
| Einwand 2: | Was ist mit Potentialfeldern? Schwerkraft oder elektrische Anziehungskaft nehmen quadratisch mit dem Abstand der beteiligten Objekte ab? Das ist doch ein nichtlinearer Zusammenhang mit abnehmenden Kräften bei zunehmendem Abstand? | |
| Antwort: | Stimmt. Aber Potentialfelder sind keine Federn. Das hindert nicht daran, daß in Potentialfeldern der Energieerhaltungssatz Gültigkeit hat. Das Thema Schwerkraft werde ich gelegentlich näher abhandeln... | |
Aufmerksame Leser werden bemerken, daß ich sie mit der Feder ein wenig aufs Glatteis geführt habe. Ich kann mir sehr gut Modelle von Federn vorstellen, die andere Kraft-Weg-Verläufe haben, wie die idealisierten hookeschen Federn aus dem Schulunterricht. Letzten Endes ist es vollkommen nebensächlich, wie eine "Feder" von ihrem inneren Mechanismus her arbeitet. Genaugenommen ist jeder Gegenstand auf irgendeine Art eine "Feder". Läßt man z.B. eine Kugel am Ende eines Stabes rotieren, so kommt die Gegenkraft im Stab, die verhindert, daß die Kugel fortgeschleudert wird, durch die Federwirkung des Stabes zustande. Wenn wir ein wenig weitergrübeln, können wir uns ein dynamisches Federmodell erarbeiten:
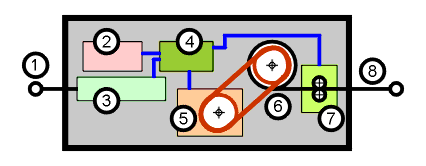
| Nr. | Bauteil |
|---|---|
1 |
Anhängeöse |
2 |
Akkumulator |
3 |
Kraftsensor |
4 |
Microcontroller/Regler |
5 |
Elektromotor-Generator-Kombination mit Haltebremse |
6 |
Seilrolle |
7 |
Längemeßeinrichtung |
8 |
Lastöse |
Wie funktioniert diese Black-Box-Feder? Wie jede andere Feder wird sie mit den Ösen 1 und 8 an den Versuchsaufbau angehängt. Der Motor 5 kann die Seilrolle 6 in beiden Richtungen bewegen. Wird das Seil herausgezogen, lädt der Motor als Generator den Akku 2. Um das Seil mit einer bestimmten Kraft einzuholen, wird aus dem Akku gespeicherte Arbeit entnommen. Der Regler 4 wertet die Zugkraft, die mit dem Sensor 3 gemessen wird und die abgerollte Seillänge (Längenmessung 7) aus und steuert entsprechend den Betrieb des Motors. Bei konstanter Zugkraft wird die Haltebremse aktiviert, sodaß der Motor die Last nicht "aktiv" halten muß. Der Regler kann über eine geeignet vorgegebene Kennlinie, die einem Kraft-Weg-Diagramm entspricht, die Zugkraft im Seil entsprechend der abgerollten Länge beeinflussen.
Das Federmodell hat gegenüber einer realen Feder einen Nachteil: wird nicht viel Gehirnschmalz in den Regler gesteckt, dann lassen sich Schwingungen nicht verwirklichen.
Mit diesem Federmodell kann offenbar jede Federkennlinie verwirklicht werden,
auch die vorhin erwähnte "inversen". Setzen wir voraus, daß
Motor/Generator und Haltebremse verlustfrei arbeiten und daß der Akku
genausoviel Elektronen hergibt, wie zuvor hineingepumpt wurden. Dennoch kann
ein Perpetuum Mobile mit dieser Feder nicht gebaut werden. Der Grund sollte
klar sein: die Arbeit, die der Feder entnommen wird, entstammt dem Akkumulator
als Energiespeicher. Wird in der Gesamtbilanz mehr entnommen, als
zurückgespeist wird, ist der Akkumulator irgendwann leer.
Mechanische Federn können ebenfalls Energie speichern. Doch geben sie
nicht mehr her, als sie gespeichert haben...
| weiter mit Physik II |
| Stand: 16.12.2002 / |
|