Geometrische Zerlegungen

---

Mündlich überliefert Feldwebel: In wieviele Teile zefällt das Gewehr? Rekrut: Kommt drauf an, wie man's hinschmeißt.

Anschweifung

Der Rekrut hat's erfaßt. Die Kunst liegt darin, das Thema auf den Boden oder in freundlicheren Kreisen auf den Tisch zu bringen und nicht gemäß den Vorschriften zu betrachten. Da wir nun mal schon beim Militär (Denkverbot) sind, hier eine Schnurrpfeiferei, die mein Vater aus dem Krieg mitbrachte und die ins Thema paßt (Denkbarriere!). Eigentlich muß man diese Sache mit Papier und Bleistift oder an der Tafel erzählen - aber ich versuche mal, sie adäquat als Text wiederzugeben:

Abschweifung

24 Pferde in 6 Waggons Ein Schütze erhält den Auftrag, 24 Pferde in 6 Eisenbahnwaggons zu verladen. Dem Soldaten ist klar, daß er rechnen muß, doch er hat in der Schule nur selten aufgepaßt. Nun steht er da und denkt "24 durch 6, 24 durch 6...."Geistesblitz!! Ein Pferd muß in jeden Waggon, sind ja mehr Pferde als Waggons. Fröhlich wird gerechnet: 24 durch 6 = 1 Rest 18 Offenbar fehlt eine Ziffer beim Ergebnis... "Rest 18, Rest 18... " Dumme Sache. Folglich doch noch Erinnerung an die Grundschule... 1 mal 6 ist 6 2 mal 6 ist 12 3 mal 6 ist 18 Aufgegangen, stimmt! 3 x 6 = 18,  die zweite, fehlende Ziffer ist 3 und folglich müssen 13 Pferde in jeden Waggon. Die Verladung beginnt und gerät - nicht ohne Grund - bereits beim ersten Eisenbahnwaggon ins Stocken. Ein Feldwebel, der vorübergeht, stellt den Schützen im militärischen Umgangston zur Rede - auf gut Deutsch: er schei**t ihn zusammen. Die Antwort: "Verzeihung, Herr Feldwebel, ich habe gerechnet! Ich habe dividiert!". Abgesehen vom Wort "dividieren" hat unser Schütze fast nichts aus der Schule mitgenommen - der Feldwebel ein klein wenig mehr. "Zeigen Sie mal her! - Hm, sieht auf den ersten Blick richtig aus...haben Sie denn die Probe gemacht?" "Jawohl, Herr Feldwebel, Probe machen! Nein, Herr Feldwebel, keine Probe gemacht!" "Mann! Sie dürfen nie dividieren, ohne hinterher die Probe zu machen!" Der Feldwebel beginnt mühsam zu rechnen: 3 mal 6 ist 18 1 mal 6 ist 6 8 und 6 ist ist 14 4 schreib' hin, 1 im Sinn 1 und 1 ist 2 "Aufgegangen, stimmt!" Der Feldwebel ist sichtlich erfreut, klopft dem Schützen lobend auf die Schulter und sagt "Ist gut, machen Sie weiter so!" Das Gedränge im ersten Eisenbahnwaggon nimmt zu. Beider Hauptmann ist zufällig zugegen, beobachtet das Treiben und stellt den Feldwebel im militärischen Umgangston zur Rede.- auf gut Deutsch: er schei**t ihn zusammen. Die Antwort: "Verzeihung, Herr Hauptmann, Der Schütze hat gerechnet" "Haben Sie auch die Probe gemacht?" "Jawohl, Herr Hauptmann, Probe gemacht!" "Zeigen Sie mal her! - Hm, sieht auf den ersten Blick richtig aus." Der Hauptmann ist ein guter Stratege, aber ein noch besserer Taktiker. Deshalb ist ihm klar, daß er sich vor seinen Subalternen keine Blöße geben darf. Der Hauptmann hat nämlich ein kleines, privates Problem: Beim Dividieren hat er in der Schule immer gefehlt und obwohl er jede Klasse fleißig mindestens zweimal besuchte, wollte man ihn nach vierzehn Jahren dort nicht mehr so recht behalten. Das kann der Hauptmann natürlich nicht zugeben, aber er geht die Sache geschickt an: "Die Rechnung und die Probe scheinen zu stimmen. Jetzt machen wir das doch mal ganz anders! Jetzt schreiben wir sechsmal die 13 untereinander und dann zählen wir das zusammen!" Regelkonform beginnt er in der rechten Spalte und murmelt vor sich hin... "3, 6, 9, 12, 15, 18..." der Hauptmann ändert die Zählrichtung und macht in der vorderen Spalte weiter: "19, 20, 21, 22, 23, 24" "Aufgegangen, stimmt!" Der Hauptmann ist sichtlich erfreut, klopft dem Schützen lobend auf die Schulter und sagt "Ist gut, machen Sie weiter so!"

Ich habe das G'schichtl mal bei einem Offiziers-/Unteroffiziersabend nach einer Wehrübung erzählt. Alle Teilnehmer folgten willig der Argumentation. Etwa zwei Drittel durchschauten nicht den Fehler. Was lernen wir daraus?

1. Wir sollten nicht allzu bereitwillig den Gedankengängen Anderer folgen. Gedankengänge können gelegentlich falsch sein...und doch so schlüssig aussehen!
2. Fakten sollten übersichtlich dargestellt werden und die Präsentation dem geistigen Horizont der Zuhörer oder Leser gerecht werden.

 Zur Sache

Es geht hier, wie die Überschrift vermuten läßt, um geometrische Zerlegungen. Man nehme ein Quadrat der Kantenlänge 8 und zerschneide es gemäß dem nachstehenden Schema

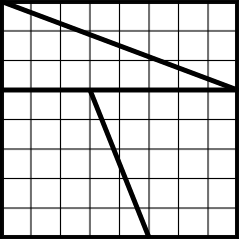
Dann werden die 4 Einzelteile zu einem 5 x 13 - Rechteck zusammengesetzt:

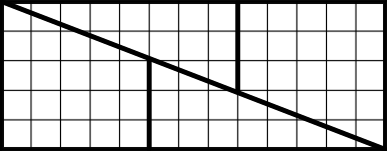
Quadrat und Recheck sind offenbar flächengleich, da sie aus denselben Teilen zusammengesetzt werden können. Wir haben "bewiesen", daß 8 x 8 = 5 x 13. Es gilt folglich 64 = 65. Wie bitte?

Das Spiel läßt sich fortsetzen. Wie wär's mit einem 13x13-Quadrat?

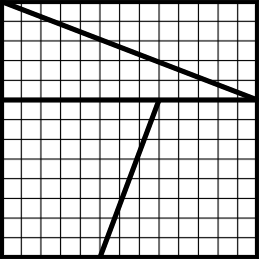
Geschickt zerlegt, läßt es sich zu einem 8 x 21-Rechteck kombinieren.

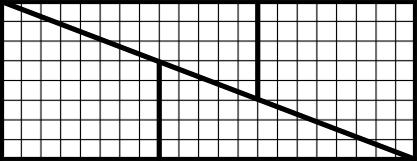
Somit ist schlüssig "bewiesen", daß 13 x 13 = 8 x 21, also 169 = 168. Das ist wie verhext! Jetzt ist das erzeugte Rechteck um eine Flächeneinheit kleiner als beim vorigen Beispiel.

Tatsächlich wurde hier elegant geschummelt. Die dicken Linien täuschen eine Genauigkeit vor, die nicht da ist.

Das Spiel läßt sich fortsetzen. Machen wir eine Tabelle auf, die die Ergebnisse zusammenfaßt. Dabei wurde die längere Kante des Rechtecks (=x) immer als Seitenlänge des nächsten Quadrates verwendet - und die Seitenlänge des Quadrates immer als kurze Kante (=y) des neuen Rechtecks.:

Kantenlänge Quadrat a	Rechteck		Fläche Quadrat	Fläche Rechteck	Flächen- differenz
	x	y
8	13	5	64	65	1
13	21	8	169	168	-1
21	34	13	441	442	1
34	55	21	1156	1155	-1
55	89	34	3025	3026	1
89	144	55	7921	7920	-1

Natürlich ist die vorige Formulierung bewußt verwirrend gehalten...

Fibonacci und die Folgen

Spätstens jetzt sollte ein wenig die Erfahrung ins Spiel kommen und sagen: "Haltauf! die Zahlenwerte sind verdächtig! 3,5,8,13,21 - alles Fibonacci-Zahlen!" Überraschender ist, daß die Ergebniswerte anscheinend immer +/-1 Defizit zu einer Quadratzahl haben; immer abwechselnd. Das gibt (hoffentlich) zu denken, zumal die Kantenlänge des Quadrates ebenfalls eine Fibonaccizahl ist.

Definition:	Die Fibonacci-Zahlen werden mit F0, F1, F2... bezeichnet. F0 = 0 F1 = 1 Fn+1 = Fn + Fn-1
Behauptung:	(Fn)2 = Fn-1 * Fn+1 + 1 für n gerade (Fn)2 = Fn--1 * Fn+1 - 1 für n ungerade

Ein verregneter Urlaubsnachmittag gab mir Gelegenheit, einen netten Induktionsbeweis für diese Behauptung zu finden.

Als Induktionsanfang mag die vorhin gezeigte Tabelle dienen - etwas verändert

n	Fn	Fn+1	Fn-1	(Fn)2	Fn+1 x Fn-1	Fn+1 x Fn-1- (Fn)2
0	0	1	--	--	--	--
1	1	1	0	1	0	-1
2	1	2	1	1	2	1
3	2	3	1	4	3	-1
4	3	5	2	9	10	1
5	5	8	3	25	24	-1
6	8	13	5	64	65	1
7	13	21	8	169	168	-1
8	21	34	13	441	442	1
9	34	55	21	1156	1155	-1
10	55	89	34	3025	3026	1
11	89	144	55	7921	7920	-1

Für den Index 0 gilt die Behauptung offenbar nicht, da es keine Fibonaccizahl F_-1 gibt. Aber ab F₁ stimmt die Sache (in der Tat würden als Induktionsanfang die Indizes 1 und 2 ausreichen). Der Beweis erfolgt in zwei Schritten. Die Lösung finden Sie hier. Erstmal sollten Sie aber schon selber denken!

Als Konsequenz aus dieser Betrachtung gibt es noch eine hübsches Frage aus der Grenzwertberechnung (goldener Schnitt!)

bekanntlich glit lim n->8 (F_n / F_n--1) = (1+sqrt5)//2

wohin konvergiert lim n-> 8 ((F_n)² - (F_n--1 * F_n+1))

Mit dem Wissen um den goldenen Schnitt läßt sich ein Qudrat so zerlegen, daß es in ein exakt flächengleiches Rechteck umgestellt werden kann:

----